Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 147

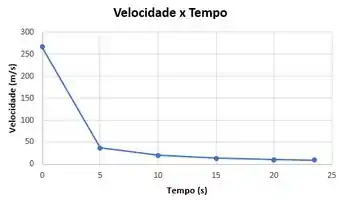
Um veículo-foguete, pesando 44.500   N e viajando a 960   k m / h , deve ser freado pelo abaixamento de uma concha para dentro de um reservatório de água. A concha tem 150   m m de largura. Determine o tempo necessário (após o abaixamento da concha até uma profundidade de 75   m m na água), para reduzir a velocidade do veículo a 32   k m / h . Trace um gráfico da velocidade do veículo em função do tempo.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = u ) ;
  4. Escoamento uniforme;
  5. Resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x - ∫ V C a r f x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não há forças de campo atuando no sistema e não a resistência, então, F B x = F S x = 0 :

- ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Então:

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Passo 3

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Para o fluxo de entrada, V   e   A possuem uma inclinação de 180°, então ρ V A = ( - ρ V A ) .

- a x ⋅ m = u 1 - ρ V A + u 2 ρ V A

Aqui, u 1 indica a velocidade relativa do fluxo de entrada, já u 2 , a velocidade relativa do fluxo de saída para as mesmas condições.

u 1 = u ;

u 2 = - u ⋅ c o s   θ .

Substituindo: m = W g e A = b ⋅ h

- a x ⋅ W g = u ⋅ ( - ρ ⋅ u ⋅ b ⋅ h ) + ( - u ⋅ cos ⁡ θ ) ⋅ ( ρ ⋅ u ⋅ b ⋅ h )

a x ⋅ W g = u 2 ⋅ ρ ⋅ b ⋅ h ⋅ ( c o s   θ + 1 )  

a x = g ⋅ u 2 ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1 W  

Passo 4

Sendo:

a x = d u d t = g ⋅ u 2 ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1 W

d u u 2 = g ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1 W   d t

∫ u 0 u d u u 2 = ∫ 0 t g ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1 W d t

Integrando temos:

1 u - 1 u 0 = g ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1 W ⋅ t

t = 1 u - 1 u 0 ⋅ W g ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1

Passo 5

Sendo:

W = 44.500   N ;

u 0 = 960 k m h = 266,67 m s ;

u = 32 k m h = 8,89 m s ;

b = 0,15   ;

h = 0,0 75   m ;

g = 9,8   m / s 2 ;

ρ = 1000   k g / m 3 ;

θ = 30 ° .

Temos:

t = 1 8,89 - 1 266,67 ⋅ 44.500 9,8 ⋅ 1000 ⋅ 0,15 ⋅ 0,075 ⋅ c o s   30 ° + 1 = 23,5   s

Passo 6

Para traçarmos um gráfico da velocidade do veículo em função do tempo, temos que isolar a velocidade do veículo:

t = 1 u - 1 u 0 ⋅ W g ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1

u = W ⋅ u 0 W + g ⋅ u 0 ⋅ ρ ⋅ b ⋅ h ⋅ c o s   θ + 1 ⋅ t = 11.866.815 44500 + 54.861,8 ⋅ t

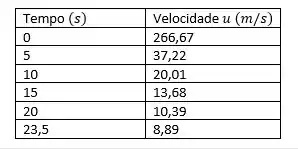
Utilizando tempos de 0 a 23,5   s :

Resposta

t = 23,5   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois grandes tanques contendo água têm pequenos orifícios de contornos lisos e arredondados e de áreas iguais. Um jato de líquido sai do tanque da esquerda. Considere que o fluxo seja uniforme e não a
Um jato de ar horizontal com 13 mm de diâmetro, e axialmente simétrico, atinge um disco estacionário vertical com 203 mm de diâmetro. A velocidade do jato é de 69 m/s na saída do bocal. Um manômetro e
Um jato uniforme de água sai de um bocal de 15 mm de diâmetro e escoa diretamente para baixo. A velocidade do jato no plano de saída do bocal é 2,5 m/s. O jato atinge um disco horizontal e escoa radia
Você abre a torneira da cozinha muito lentamento, de modo que um filete de água escoa para a pia. Você nota que o escoamento é laminar e que isso se reforça para os primeiros 50 mm de descida. Para me
Um disco de 2 kg é restringido horizontalmente, mas está livre para mover na direção vertical. O disco é atingido por baixo por um jato vertical de água. Na saída do bocal, a velocidade e o diâmetro d