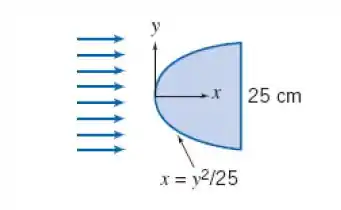
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 7 , 5m / s . O ar está a 20 ° C e a 101,3 k P a . (Note que a forma da placa é dada por x = y 2 / 25 , em que x e y são dados em centímetros)

2 F D = 3,95 ⋅ 10 - 3 N (força total em ambos os lados)

Enunciado

O enunciado diz que o escoamento é laminar, e pede para calcularmos a força de arrasto. Como ele é laminar em uma placa plana, valem as relações:

Ele também dá ums informações importantes:

Velocidade de corrente livre:

A forma da placa:

Temos o ar a , o que implica em e

A força total de arrasto pode ser definida como:

Então precisamos de uma expressão para .

Como a gente encontra isso? Usando as equações da camada limite:

Uhul! Conseguimos!

Agora, começamos a montar a nossa integral:

Repara que a nossa largura muda conforme andamos na direção do fluxo, isso é, conforme variamos . Por isso, podemos escrever:

Como achamos essa largura em função de ? Temos que:

Onde é o comprimento percorrido pelo fluído na placa.

A placa tem a forma da parábola:

O que diz para gente que nossa função para largura tem que ter uma raiz quadrada. Aí usando essas condições acima, podemos dizer que:

Reescrevendo:

Sabendo que

Precisamos substituir os dados do problema, mas quem é ?

Repara que é o valor de quando . Logo:

Sendo :

Isso se a gente pensar na força em um lado só da placa. Pensando na força aplicada em ambos os lados, é só multiplicar por :

(força total em ambos os lados)