Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 62
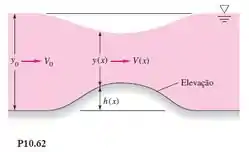
Considere o escoamento em um canal largo sobre uma elevação, como na Figura P10.62. Podemos avaliar a variação na profundidade da água ou transição, admitindo escoamento sem atrito. Use a equação da continuidade e a equação de Bernoulli para mostrar que
A depressão da superfície da água é realística na Figura P10.62? Explique em quais condições a superfície poderia se elevar acima de sua posição a montante.
Passo 1
Lets bora, parceria!
Bora usar uma expressão de energia para resolver essa questão, veja:
Vamos simplificar e diferenciar, assim:
Assim,
Se na frente da elevação, teremos um aumento no nível da água, assim o fluído é supercrítico, podendo sim ser uma situação realística.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Considere o canal em forma de V da Figura PA10.7, com um ângulo arbitrário θ. Faça uma análise da continuidade e da quantidade de movimento para uma pequena perturbação δy que a velocidade de propagaç
Determine a profundidade crítica do canal de tijolos no Problema P10.34 para as larguras de 1,22 e 2,44 m. Os escoamentos normais são subcríticos ou supercríticos?
Uma ponta de lápis penetrando na superfície livre de um canal retangular cria uma onda em formato de cunha de 25° de semiângulo, como na Figura P10.50. Se a superfície do canal for de aço pintado e a
Um rio largo, com leito em terra limpa, tem uma vazão q = 13,94m 3 / ( s ⋅ m ) . Qual a profundidade crítica? Se a profundidade real for de 3,66 m, qual será o número de Froude do rio? Calcule a decli
Para o escoamento do rio do Problema P10.48, encontre a profundidade y 2 que tem a mesma energia específica que a profundidade dada y 1 = 3,66m . Elas são chamadas de profundidades conjugadas. Qual é