Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 41
Considere o escoamento de um fluido permanente, incompressível, bidimensional em um duto convergente, com paredes retas. A vazão em volume é e a velocidade ocorre somente na direção radial, com ur sendo uma função apenas de r. Seja b a largura perpendicular à página. Na entrada do duto convergente (r=R), ur = ur(R).
Considerando escoamento sem viscosidade em todos os pontos, gere uma expressão para ur como uma função de r, R e ur(R) somente. Faça um desenho de como seria o perfil de velocidade no raio r se o atrito não fosse desprezado (isto é, um escoamento real) com a mesma vazão em volume.
GABARITO 45
Passo 1
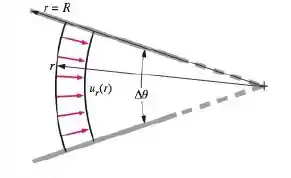
Primeira coisa que a gente precisa lembrar é que se o escoamento fosse sem viscosidade, não poderíamos forçar uma condição de não deslizamento nas paredes do duto.
Em qualquer localidade r, o fluxo volumétrico será dado por:
Onde a variação de ângulo pode ser vista na figura acima, beleza?
Passo 2
Isolando nosso amiguinho ur:
Para r = R, a gente vai ter o seguinte então:
Agora, malandramente a gente vai pegar essa equação ur(R) isolar a vazão volumétrica eeeee substituir na equação ur, e vamos ter:
Passo 3
Para um escoamento real oficial, a gente tem que levar em consideração a condição de não deslizamento nas paredes, beleza? E outra coisa interessante é lembrarmos que com a diminuição da área transversal de escoamento, a velocidade de escoamento deve aumentar, por isso no centro do duto a velocidade deve ser maior. Portanto é provável que o perfil seja nesse formato aí de cima!!!