Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 22
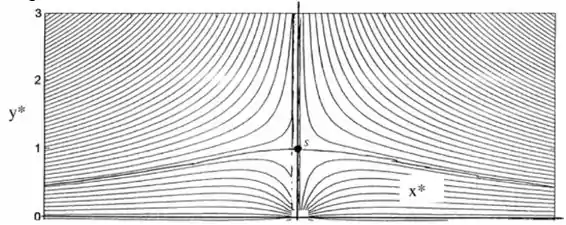
Considere o escoamento não viscoso de estagnação, (ver a Figura 8.19b) superposto a uma fonte de intensidade m na origem. Trace as linhas de corrente resultantes no semiplano superior, usando a escala de comprimento . Dê uma interpretação física do padrão de escoamento.
Passo 1
Bora pra mais uma!
A soma do fluxo de estagnação mais uma fonte de linha na origem é:
Para plotar o gráfico, vamos definir alguns parâmetros:
Substituindo estes parâmetros na primeira equação, obtemos:
Daí, podemos plotar o gráfico, para isto, foi utilizado a ferramenta pyplot do python, mas pode utilizar o software de sua preferência.
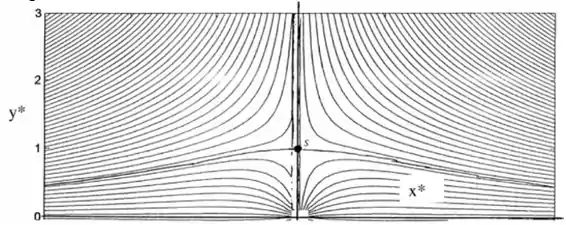
Resposta
O grafico plotado representa o fluxo de estagnação em direção a uma elevação de altura.
Exercícios de Livros Relacionados
Um dos padrões de escoamento em um canto da Figura 8.19 é dado pela função corrente cartesiana ψ = A 3 y x 2–y 3 . Qual deles? A correspondência pode ser provada por meio da Equação ( 8.53 ) ?
O escoamento potencial em torno de uma cunha com semiângulo θ conduz a uma aplicação importante da teoria de camada-limite laminar chamada de escoamentos de Falkner-Skan [ 15 ,p .239 – 245 ] . Seja x
Investigue o potencial complexo f z = A cosh [ p ( z / a ) ] e trace as linhas de corrente dentro da região mostrada na Figura P 8.69 . Que palavra hifenizada (de origem francesa) pode descrever tal
A velocidade não viscosa ao longo da cunha do Problema P 8.65 tem uma forma analítica U x = C x m , em que m = n– 1 e n é o expoente na Equação ( 8.53 ) . Mostre que, para quaisquer C e n , o cálculo
Combine o escoamento de estagnação da Figura 8.19 b com uma fonte na origem: f z = A z 2 + m ⋅ ln z Trace as linhas de corrente para m = A L 2 , sendo L uma escala de comprimento. Interprete.