Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 96
Suponha que uma esfera com um orifício de estagnação simples é usada como velocímetro. A pressão nesse orifício é usada para calcular a velocidade U da corrente, mas há erros se a corrente não estiver perfeitamente alinhada com as linhas de corrente mais próximas. Usando a teoria de escoamento invíscido e incompressível, plote o erro percentual da velocidade de corrente como uma função do desalinhamento do ângulo . Em qual ângulo o erro será de 10%?
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é DESENHAR!!!
Vamos considerar e assumir que o medidor de pressão lê a diferença entre a pressão no orifício e a pressão ambiente . Quando perfeitamente alinhado, nós temos a pressão de estagnação a qual pode ser calculada como sendo:
Passo 2
Se nós estivermos desalinhados por um ângulo qualquer, haverá uma velocidade V não nula no orifício, dado pela equação 8.100 do livro, tal que:
Usando a equação de Bernoulli, temos que:
Esse resultado que encontramos no passo 2 é quando o instrumento lerá um valor menor numa quantidade equivalente a
Passo 3
Note que então para um erro de 10%, temos que ter
Substituindo isso na nossa equação do passo 2, teremos que
Passo 4
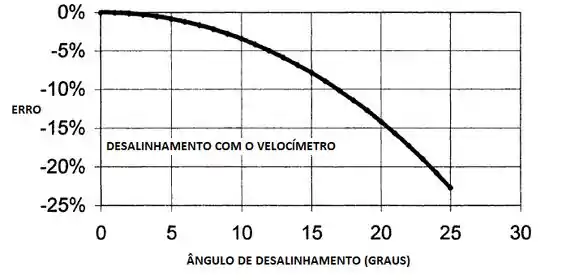
Um gráfico de erro em função de pode ser feito e montado como mostrado abaixo!!
