Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 33

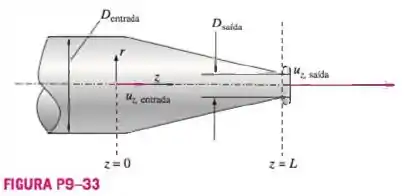
Considere o escoamento permanente de água através de um bocal axissimétrico de mangueira de jardim (Figura P9-33).A componente axial da velocidade aumenta linearmente de u e n t r a d a a u s a í d a conforme está representado na figura. Entre z =   0 e z = L , a componente é dada por u z = u z , e n t r a d a + u z , e n t r a d a - u , s a i d a L z . Encontre uma expressão para a componente da

velocidade radial u r entre z   =   0 e z   =   L . Você pode ignorar os efeitos de atrito nas paredes.

Passo 1

Bora lá entender essa questão!

A gente tem um escoamento permanente, vamos considerar que esse escoamento também seja incompressível e que ele seja axialmente simétrico!

Mas o que é isso?

Isso é, se a gente partir a mangueira no meio, no sentido horizontal devemos ver o mesmo comportamento do fluido tanto em cima, quanto em baixo! Belezinha?!

Vamos usar o sistema de coordenadas cilindrico para a equação de continuidade:

1 r ∂ r u r ∂ r + ∂ u z ∂ z = 0

E agora temos a componente de velocidade dada no enunciado:

u z = u z , e n t r a d a + u z , e n t r a d a - u , s a i d a L z

Passo 2

Você viu que a velocidade u z aparece na equação da continuidade? Mas ela aparece sendo derivada, então vamos derivar a equação que o enunciado nos deu!

u z = u z , e n t r a d a + u z , e n t r a d a - u , s a i d a L z

∂ u z ∂ z = u z , e n t r a d a - u , s a i d a L

Passo 3

Queremos a componente u r , certo? Então vamos isolar ela na equação na continuidade e substituir ∂ u z ∂ z :

∂ r u r ∂ r = - r ∂ u z ∂ z

∂ r u r ∂ r = - r u z , e n t r a d a - u , s a i d a L

Mas o que a gente quer de verdade é u r , vamos então isolar ele para integrar:

∫ ∂ r u r = ∫ - r u z , e n t r a d a - u , s a i d a L ∂ r

Integrando:

r u r = - r 2 2 u z , e n t r a d a - u , s a i d a L + f ( z )

Isolando:

u r = - r 2 u z , e n t r a d a - u , s a i d a L + f z r

Viu esse f ( z ) que apareceu? Ele aparece porque a nossa integral não tinha os limites de integração. E como a nossa integral é parcial a constante deve ser uma função de z !

Se você tiver duvidas é só pegar o u r que a gente terminou de achar, derivar ele em relação a r e substituir na equação da continuidade que a gente viu lá em cima!! Essa é uma boa prova dos nove pra ver se a conta foi feita certinha!

Agora para finalizar precisamos saber quem é f ( z ) !!

O único valor de r que conhecemos é r = 0 no centro da mangueira, quando fazemos essa substituição f z vai para infinito (como qualquer número ou função dividida por zero), isso só não acontece se considerarmos f z = 0 , então:

u r = - r 2 u z , e n t r a d a - u , s a i d a L

Resposta

u r = - r 2 u z , e n t r a d a - u , s a i d a L

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Que restrições ou condições são impostas na função corrente Ψ de maneira que ela satisfaça exatamente a equação da continuidade bidimensional incompressível por definição? Porque essas restrições são
Considere o seguinte campo de velocidade permanente, tridimensional em coordenadas cartesianas: V →=( u ,v ,w )=a x y 2—b i →+c y 3 j →+d x y k → , onde a, b,c ,ed são constantes. Sob que condições es
Imagine escoamento incompressível, permanente, bidimensional que é puramente radial no plano x y ou r θ . Em outras palavras, a componente de velocidade u r é diferente de zero, mas u θ é zero era tod
A componente de velocidade u de um campo de escoamento permanente, bidimensional, incompressível é u =a x+b , onde a e b são constantes. A componente de velocidade v édesconhecida. Encontre uma expres
A componente de velocidade u de um campo de escoamento permanente, bidimensional, incompressível é u =a x+b y , onde a e b são constantes. A componente de velocidade v édesconhecida. Encontre uma expr