Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 30

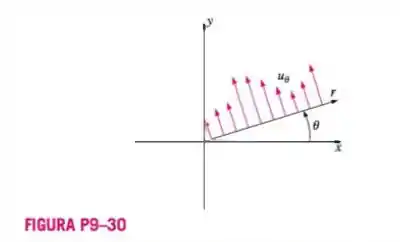
Imagine escoamento incompressível, permanente, bidimensional que é puramente circular no plano x y ou r θ . Em outras palavras, a componente de velocidade u θ é diferente de zero, mas

u r é zero era todos os pontos (Figura P9-30). Qual é a forma mais geral da componente u θ de velocidade que não viola a conservação da massa?

Passo 1

Vamos lá!! O enunciado diz que o escoamento é incompressível e permante então ele tem que obedecer a equação da continuidade!

Vamos escrever a equação da continuidade para um escoamento bidimensional usando as coordenadas cilindricas:

1 r ∂ r u r ∂ r + 1 r ∂ u θ ∂ θ = 0

Como o enunciado disse, u r = 0 , então:

∂ u θ ∂ θ = 0

Como a derivada é igual a zero, logo r u θ deve ser uma constante, mas como aqui estamos falando de uma derivada parcial, vamos dizer que essa constante é função de r ;

u θ = f ( r )

Prontinho!!!! Essa é a forma mais geral da componente u θ de velocidade que não viola a conservação da massa!

Resposta

u θ = f ( r )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento permanente, incompressível, paralelo, laminar de um fluido viscoso descendo entre duas paredes verticais infinitas (Fig. P9–82). A distância entre as paredes é h, e a gravidade
Os dois primeiros termos viscosos no componente θ da equação de Navier -Stokes (Eq. 9-62c) são μ 1 r ∂ ∂ r r ∂ u θ ∂ r - u θ r 2 . Expanda essa expressão o máximo possível usando a regra do produto, p
Um líquido newtoniano incompressível está confinado entre dois cilindros circulares concêntricos de comprimento infinito - um cilindro interno sólido de raio R i e um cilindro oco, permanente, externo
Para o fluido descendo entre duas paredes verticais paralelas (Prob. 9–82), encontre uma expressão para a vazão em volume por unidade de largura V ˙ L em função de ρ ,μ ,heg . Compare seu resultado co
Considere o seguinte campo de velocidade permanente, bidimensional, incompressível: V → = u ,v = a x + b i ^ + - a y + c j ^ , onde a ,bec são constantes. Calcule a pressão em função de x e y.