Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 79

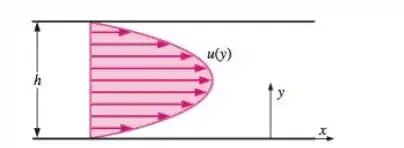
Considere o escoamento de Poiseuille totalmente desenvolvido e bidimensional – o escoamento entre duas placas paralelas finitas separadas pela distância h , com as placas superior e inferior fixas, e um gradiente de pressão forçado d P d x movendo o escoamento como ilustra a figura P 4 - 79 . ( d P d x é constante e negativo). O escoamento é incompressível, em regime permanente e bidimensional no plano x y .   As componentes da velocidade são dadas por:

u = 1 2 μ d P d x y 2 - h y

v = 0

Onde μ   é a viscosidade do fluido. Esse escoamento é rotacional ou irrotacional? Se ele for rotacional, calcule a componente da vorticidade na direção z .   As partículas de fluido desse escoamento giram no sentido horário ou anti-horário?

Passo 1

Eae gente, tubo beleza? Bora pra mais uma questão de Mecânica dos Fluidos. Primeiramente, se a vorticidade não é nula, o escoamento só pode ser rotacional. Portanto, podemos calcular a componente z da vorticidade, que é dada por:

ζ z = ∂ v ∂ x - ∂ u ∂ y = 0 - 1 2 μ d P d x   2 y - h = - 1 2 μ d P d x 2 y - h

Como a vorticidade é diferente de zero, esse fluxo é rotacional. Além disso, na metade inferior do fluxo ( y   < h   /   2 ) a vorticidade é negativa (observe que d P / d x é negativa).

Assim, as partículas giram no sentido horário na metade inferior do fluxo. Da mesma forma, as partículas giram no sentido anti-horário na metade superior do fluxo.

Resposta

Fluido Rotacional

ζ z = ∂ v ∂ x - ∂ u ∂ y = 0 - 1 2 μ d P d x   2 y - h = - 1 2 μ d P d x 2 y - h

As partículas giram no sentido horário na metade inferior do fluxo. Da mesma forma, as partículas giram no sentido anti-horário na metade superior do fluxo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a forma geral do teorema de transporte de Reynolds (TTR) dada por d B s i s t d t = d d t ∫ ρ b d V + ∫ ρ bV r → ∙ n → d A onde V r → é a velocidade do fluido com relação à superfície de con
Combine seus resultados do Problema 4 - 72 para formar o tensor de taxa de deformação bidimensional ε i j . ε i j = ε x x ε x y ε y x ε y y Os eixos x e y são principais?
Para o escoamento de Couette da Figura P 4 - 71 , calcule as taxas de deformação linear nas direções x e y , e calcule a taxa de deformação por cisalhamento ε x y .
Compare os resultados do Problema 4 - 79 e 4 - 84 e comente sobre a taxa de deformação linear na direção x .