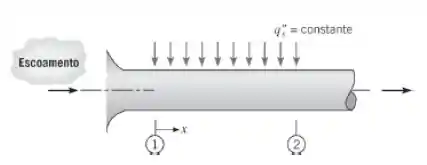
Considere o escoamento em um tubo circular. No comprimento da seção de teste (entre 1 e 2), um fluxo térmico constante é mantido.

1. Para os dois casos a seguir, esboce a temperatura superficial e a temperatura média do fluido em função da distância ao longo da seção de teste x. No caso A, o escoamento encontra-se fluidodinâmica e termicamente plenamente desenvolvido. No caso B, o escoamento não está desenvolvido.
2. Supondo que o fluxo superficial e a temperatura média na alimentação sejam idênticos em ambos os casos, indique se a temperatura média na saída, , para o caso A será maior, igual ou menor do que o valor de para o caso B. Explique sucintamente o porquê.

Animados para continuar?

Eu espero que sim !!

Esta é bem gostosa, mas exige muitos conceitos!

Quando nós temos um fluxo de calor constante para a superfície podemos dizer que:

Quando integramos:

O fluxo de calor é convectivo, portanto:

Isso nos trás uma relação entre as duas, certo?

Beleza!!

Quando o escoamento é completamente desenvolvido o coeficiente convectivo é constante, então à medida que a distância x aumenta, a diferença, permanece igual. Mas como é linear, também será!

Quando temos o escoamento em desenvolvimento, o coeficiente vai decrescer com a distância até atingir o desenvolvimento completamente desenvolvido.

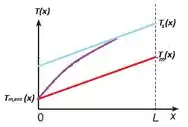
Postando estes dados em um gráfico:

Aqui, a curva vermelha representa a reta para A curva em azul representa para o escoamento completamente desenvolvido, percebem que a distância entre as temperaturas permanece, certo?

A linha em roxo representa o escoamento em desenvolvimento, alcançando o escoamento completamente desenvolvido quando