Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 100

Sejam o sistema de resfriamento de ar e as condições do Problema 8.31 , mas com um comprimento do tubo especificado de L   =   15   m .

(a) Qual é a temperatura de saída do ar, T m , s a i ? Qual é a potência necessária no soprador?

(b) O coeficiente convectivo associado ao escoamento do ar pelo tubo pode ser dobrado através da inserção de uma mola helicoidal ao longo do comprimento do tubo para romper as condições do escoamento próximo à superfície interna. Se tal esquema de intensificação da transferência de calor for adotado, qual é o respectivo valor de T m , s a i ? O uso do interno

não virá sem um aumento correspondente na potência requerida no soprador. Qual é a potência necessária se o fator de atrito for aumentado em 50 % ?

(c) Após uma exposição prolongada à água, uma fina camada de matéria orgânica se forma na superfície externa do tubo e sua resistência térmica (para uma área unitária da superfície externa) é de R t ,   e ' ' =   0,050   m 2 · K / W . Qual é o valor correspondente de T m , s a i , sem considerar o interno da parte ( b ) ?

Passo 1

Vamos lá! Nosso problema pede a temperatura de saída a potência e as consequências da variação de potência, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.

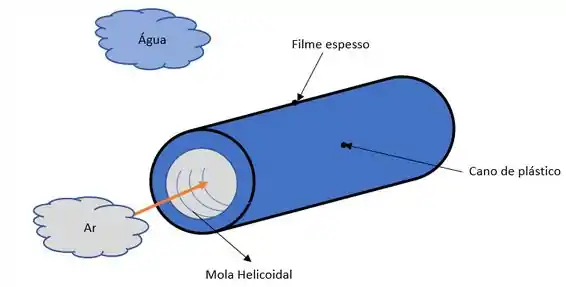
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - R e g i m e   p e r m a n e n t e

I I - T r a n s f e r ê n c i a   d e   c a l o r   e n t r e   a   p i p a   e   o   a r   d e s p r e z í v e l   e m   s e ç õ e s   v e r t i c a i s

I I I - A r   s e   c o m p o r t a   c o m o   g á s   i d e a l   s e m   v a r i a ç ã o   d e   p r e s s ã o   o u   d i s s i p a ç ã o   v i s c o s a

I V - I n t e r i o r   d a   t u b u l a ç ã o   s e m   a   m o l a   é   l i s a

V - E s p e s s u r a   d o   r e v e s t i m e n t o   d e s p r e z í v e l

V I - P r o p r i e d a d e s   c o n s t a n t e s

Passo 2

(a)

Vamos lá, vamos usar os dados da tabela A - 4 para o ar, para a temperatura interna e para a temperatura média, usando a equação 8.45 a :

T ∞ - T m ,   s a i T ∞ - T m ,   e n t r a = e - U - A s m ˙ c p

Das equações 3.36 e 3.37 .

U A s - 1 = R t o t = 1 h - i π D i L + ln ⁡ D e D i 2 π L k + 1 h 0 π D 0 L

Com m ˙ = ρ i V i = 0,0289   k g m 3 e R e A = 4 m ˙ π D i μ = 13.350 , temos que o escoamento da tubulação é turbulento. Com L D i = 100 , nós podemos assumir que o escoamento está completamente desenvolvido no encanamento, da equação 8.60 .

h i - = k a D i ⋅ 0,023 R e A 4 5 ⋅ P r 0,3 = 0,0261   W m ⋅ K 0,15   m ⋅ 0,023 13.350 4 5 ⋅ 0,707 0,3

h i - = 7,20   W m 2 ⋅ K

Assim:

R t o t = 1 7,2 ⋅ π ⋅ 0,15 ⋅ 15 + ln ⁡ 0,17 0,15 2 π ⋅ 15 ⋅ 0 , 15 + 1 1500 ⋅ π ⋅ 0,17 ⋅ 15

R t o t = 0,0286 K W

Como U A s - 1 = R t o t , U A s = 35 W K temos:

T ∞ - T m ,   s a i T ∞ - T m ,   e n t r a = e - U - A s m ˙ c p

Organizando a equação temos:

T m ,   s a i = T m ,   e n t r a - T ∞ ⋅ e - U - A s m ˙ c p + T ∞

Substituindo tudo chegamos:

T m ,   s a i = 20,6   ° C

Misturando as equações 8.21 e 8.22 com f = 0,0291 e u m ,   i = 1,415   m / s

P ≈ f ⋅ ρ i u m ,   i 2 2   D i L ⋅ V ˙ i = 0,0291 ⋅ 1,155 ⋅ 1,415 2 2   0,15 15 ⋅ 0,025 = 0,84   W

Passo 3

(b)

Com h c p = 2 h i = 14,4 W m 2 ⋅ K , a resistência a convecção é reduzida de 0,0196   K / W para 0,0098   K / W , assim a resistência total vai ser reduzida de 0,0286   K / W para 0,0188   K / W .

Como R t o t = U A s - 1 , U A s = 53,2   W / K .

Assim a temperatura é:

T m ,   s a i = 18 , 9   ° C

Se a força de atrito for aumentada em 50 % temos:

f p = 1,5 f

Logo nossa potência será:

P ≈ f ⋅ ρ i u m ,   i 2 2   D i L = 0,126   W

Passo 4

(c)

Com a malha sendo formada de matéria orgânica temos:

R t ,   c = R t , c ' ' π D e L = 0,05 π ⋅ 0,17 ⋅ 15 = 0,0062   K / W

Assim a resistência total será R t o t = 0.0348   K / W e U A s = 28.7 W /   K , por fim nossa temperatura de saída será:

T m ,   s a i = 21 , 5   ° C

Isso é tudo pessoal! \o/

Resposta

(a) T m ,   s a i = 20,6   ° C , P = 0,84   W

(b) T m ,   s a i = 18 , 9   ° C , P = 0 , 126   W

(c)   T m ,   s a i = 21,5   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao utilizar análise dimensional, Kutateladze [9] postulou que o fluxo térmico crítico varia com o calor de vaporização, com a massa específica do vapor, com a tensão superficial e com o parâmetro do d
Um cilindro, com diâmetro de 120m m e a 1000K , é imerso em água saturada a 1a t m . Descreva o processo de têmpera e estime a taxa máxima de remoção de calor, por unidade de comprimento, durante o pr
Estime a corrente elétrica que provocará a queima (derretimento) de um fio de níquel com 1 mm de diâmetro submerso em água à pressão atmosférica. A resistência elétrica do fio é de 0,129Ω / m .
Um fio horizontal de platina, com 1m m de diâmetro e emissividade ε=0,25 , opera em água saturada a pressão de1a t m . (a) Qual será o fluxo térmico na superfície se sua temperatura superficial for T
Um elemento aquecedor de 5m m de diâmetro é mantido com uma temperatura superficial de 350 ° C , quando imerso horizontalmente em água sob pressão atmosférica. A cobertura do elemento é de aço inoxidá