Ar atmosférico entra na seção aquecida de um tubo circular a uma vazão de e a uma temperatura de 20°C. O tubo têm um diâmetro D = 50 mm e condições plenamente desenvolvidas, com , estão presentes ao longo de todo o comprimento, L = 3 m.
- Para o caso de fluxo térmico na superfície uniforme e igual a , determine a taxa total de transferência de calor q e a temperatura média do ar que deixa o tubo, . Qual é o valor da temperatura superficial no início da seção aquecida, , e na saída, ? Esboce as variações axiais de e . Na mesma figura, esboce também (qualitativamente) as variações axiais de e para o caso mais realista no qual o coeficiente de transferência de calor local varia com x.
- Se o fluxo térmico na superfície variar linearmente em função de x, na forma , quais serão os valores de q, , e ? Esboce as variações axiais de e . Na mesma figura, também esboce (qualitativamente) as variações axiais de e para o caso mais realista no qual o coeficiente de transferência de calor local varia com x.
- Para as duas condições de aquecimento descritas nas partes (a) e (b), represente graficamente as temperaturas média do fluido e superficial, e , respectivamente, como funções da distância ao longo do tubo. Qual será o efeito sobre as distribuições de temperaturas de uma quadruplicação do coeficiente de transferência de calor?
- Para cada tipo de processo de aquecimento, quais são os fluxos térmicos necessários para se obter uma temperatura de saída do ar de 125°C? Represente graficamente as distribuições de temperaturas.
Passo 1
Bora continuar?!
Vamos ver o que temos aqui?
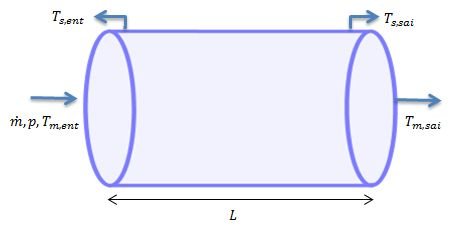
Na letra (a) nós queremos calcular a taxa total de transferência de calor q e a temperatura média do ar que deixa o tubo, , ok?
Sabemos que a taxa de transferência de calor pode ser calculada em função do fluxo térmico, :
Onde é a área superficial do tubo.
O problema nos disse:
Com isso nós conseguimos calcular fácil o calor, certo?
E agora vamos achar a temperatura média da saída, certo?
Como a temperatura do fluido muda devido a transferência de calor que o tubo recebe:
Isolando a temperatura de saída, que é o que queremos:
Ainda não temos o para o ar, mas se nós assumirmos que a temperatura de saída será próximo de 100°C:
Olhando a tabela A.4 e interpolando para esta temperatura:
Substituindo:
Passo 2
Mas a letra (a) não pediu só isso, ela também que as o valor da temperatura superficial no início da seção aquecida, , e na saída,
Como a superfície está recebendo fluxo térmico, podemos usar a lei do resfriamento nos diz que:
Rearranjando:
Substituindo:
E como se não bastasse a letra (a) ainda pediu mais!! Esboçar as variações axiais de e !
Quando nós temos um fluxo de calor constante para a superfície podemos dizer que:
Quando integramos:
O fluxo de calor é convectivo, portanto:
Isso nos trás uma relação entre as duas, certo?
Beleza!!
Quando o escoamento é completamente desenvolvido o coeficiente convectivo é constante, então à medida que a distância x aumenta, a diferença, permanece igual. Mas como é linear, também será!
Quando temos o escoamento em desenvolvimento, o coeficiente vai decrescer com a distância até atingir o desenvolvimento completamente desenvolvido.
Postando estes dados em um gráfico:
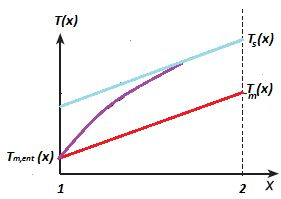
Aqui, a curva vermelha representa a reta para A curva em azul representa para o escoamento completamente desenvolvido, percebem que a distância entre as temperaturas permanece constante, certo?
A linha em roxo representa o escoamento em desenvolvimento, alcançando o escoamento completamente desenvolvido quando
Passo 3
A letra (b) nos diz para calcular os valores de q, , e , quando:
Sabemos do Passo 1 que:
Se:
Então:
Substituindo:
E integrando:
Substituindo:
E para o calor nós faremos a mesma coisa:
Substituindo:
Passo 4
Ainda precisamos achar e certo?
Já sabemos que:
Então:
Quando
Quando
Ainda temos que esboçar as variações axiais de e !
Lembrando que:
Nossa equação ficará assim:
Como queremos uma função para , o que precisamos ?
Integrar, certo?
Isolando a temperatura no ponto
Uma parábola em relação a distância,
Mas nós também queremos saber como se comporta e, para isso, nós vamos usar a equação para a troca de calor convectivo:
Isso nos trás uma relação entre as duas, certo?
Beleza!!
Quando o escoamento é completamente desenvolvido o coeficiente convectivo é constante, então à medida que a distância x aumenta, a diferença, também vai aumentar de maneira linear.
Quando temos o escoamento em desenvolvimento, o coeficiente vai decrescer com a distância até atingir o desenvolvimento completamente desenvolvido.
Postando estes dados em um gráfico:

Aqui, a curva vermelha representa a parábola para A curva em azul representa para o escoamento completamente desenvolvido, percebem que a distância entre as temperaturas aumenta, certo?
A linha em roxo representa o escoamento em desenvolvimento, alcançando o escoamento completamente desenvolvido quando
Passo 5
Na letra (c) nós vamos representar, para as duas condições de aquecimento descritas nas partes (a) e (b), graficamente as temperaturas média do fluido e superficial, e como funções da distância ao longo do tubo.
Da letra (a) nós temos que:
Vamos ver os resultados:

E colocando no gráfico pra ficar toop:
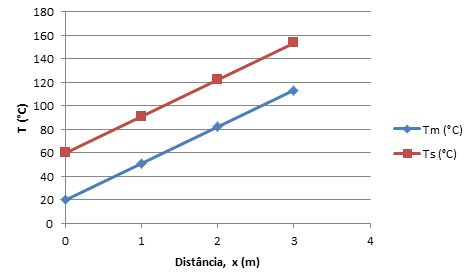
Para a letra (b)
Vamos ver os dados:

Colocando no gráfico:
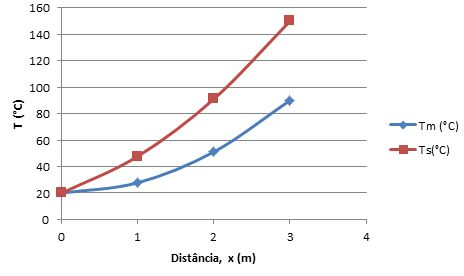
Passo 6
Mas ainda não finalizamos, certo?
Vamos para letra (d), quais são os fluxos térmicos necessários para se obter uma temperatura de saída do ar de 125°C?
Para a letra (a):
Para a letra (b):
Caramba, esta foi pra acabar com o pequi de Goiás !!
