Considere a esterilização do produto farmacêutico do Problema . Para evitar qualquer possibilidade de aquecimento do produto até uma temperatura inaceitavelmente alta, vapor de água a pressão atmosférica é condensado no exterior do tubo no lugar do aquecedor por resistência, fornecendo uma temperatura na superfície uniforme, .
(a) Para as condições do Problema , determine o comprimento de tubo reto, , que seria necessário para aumentar a temperatura média do produto farmacêutico de para ?
(b) Analise a substituição do tubo reto por uma serpentina caracterizada por um diâmetro de serpentina e um passo de . Determine a altura total da serpentina, (isto é, o produto do passo pelo número de voltas), necessária para elevar a temperatura média do fármaco até o valor desejado.
(c) Calcule a queda de pressão no tubo reto e na serpentina.
(d) Calcule a taxa de condensação do vapor.
Passo 1
Vamos lá! Nosso problema pede o comprimento do tubo reto e as consequências de troca-lo por uma serpentina, mas antes vamos fazer um esboço do nosso problema para facilitar nossa vida.
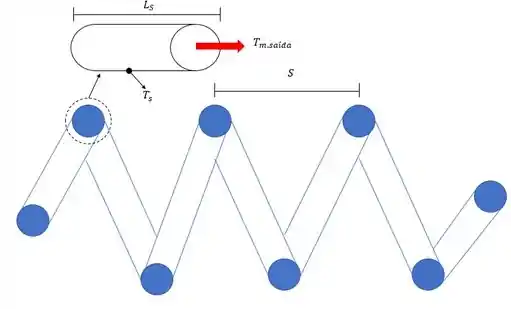
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Vamos lá, usando a tabela para a vapor d’água, com temperatura de , e os dados apresentados no problema :
Seguindo o raciocínio da questão sabemos que o escoamento é laminar pras duas situações, com , assim a relação de Hausen, temos:
Organizando e substituindo:
Usando o perímetro podemos rescrever a equação , assim temos:
Combinando as equações e e substituindo pelos valores numéricos temos:
Passo 3
(b)
Primeiro temos que calcular o comprimento do tubo para calcularmos o número de voltas da serpentina temos:
Como da equação temos:
Assim a equação fica:
Como , .
Seguindo a mesma lógica do item da letra (a) usando a equação temos:
Assim:
Estamos quase terminando a letra (b), temos que o número de voltas da serpentina:
Por fim calculando o comprimento da serpentina
Passo 4
(c) Usando a consideração , temos da equação e para calcularmos a queda de pressão.
Para a serpentina temos da equação 8.75b.
Passo 5
(d)
A taxa de condensação é dada por:
Da tabela do vapor d’água temos .
Isso é tudo pessoal! \o/

Resposta
(a)
(b)
(c) ,
(d)