O livro de receitas de culinária Betty Crocker’s Cookbook informa que leva horas e minutos para assar de costela inicialmente a em um forno mantido a . Recomenda-se que um termômetro de carne seja usado para controlar o cozimento e considera-se que as costelas estão “mal passadas” quando o termômetro inserido no centro da parte mais espessa da carne registra . A costela pode ser tratada como um objeto esférico homogêneo com propriedades , , e . Determine o coeficiente de transferência de calor na superfície da costela; a temperatura da superfície externa da costela quando estiver “mal passada” e a quantidade de calor transferido para a costela. Utilizando os valores obtidos, preveja o tempo necessário para assar a costela até estar “no ponto”, o que ocorre quando a parte interna da costela atinge a temperatura de . Compare o resultado com o valor previsto de horas e minutos.
Se a costela assada for colocada sobre um balcão por cerca de minutos antes de ser cortada, recomenda-se que seja retirada do forno quando o termômetro registrar cerca de abaixo do valor recomendado, pois a costela continua a cozinhar mesmo depois que é retirada do forno. Você concorda com essa recomendação?
Passo 1
Dados fornecidos no enunciado:
Tempo de forno: horas e minutos
Massa da costela:
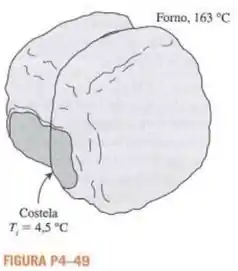
Temperatura inicial:
Temperatura no forno: .
Temperatura final na parte espessa da carne:
Densidade da carne:
Calor específico:
Condutividade térmica da carne:
Difusividade térmica da carne:
Passo 2
a) Para resolver essa questão, vamos começar calculando o volume do assado.
Aqui, é o volume do assado, é a massa do assado e é a densidade do assado. Substituindo pelos valores fornecidos, temos:
Vamos considerar o assado como sendo uma esfera. Assim podemos calcular o raio do assado da seguinte maneira:
Aqui é o raio do assado. Substituindo o volume encontrado, temos:
Passo 3
Agora, vamos encontrar o número de Fourier usando a seguinte expressão:
Substituindo pelos dados fornecidos, temos:
Como o Fourier está um pouco abaixo do valor de , portanto, a solução aproximada de termo único (ou os gráficos de temperatura transitória) ainda pode ser usada, com o entendimento de que o erro envolvido será um pouco mais de 2%.
Passo 4
A solução aproximada com um termo para esfera pode ser escrita da seguinte maneira.
Aqui, é a temperatura do assado no centro (parte mais espessa), é a temperatura inicial, é a temperatura no forno, e são as constantes. Substituindo os valores conhecido ficamos com a seguinte equação:
Passo 5
Precisamos encontrar valores para e que satisfaça a equação encontrada no passo anterior. Podemos escrever a equação de uma forma que fique mais facil a visualização. Assim temos:
Os valores para e precisão satisfazer a equação acima. Podemos usar o método de tentativa e erro para poder obtê-los. Se olharmos na tabela 4-2, os valores que irão satisfazer a equação são e .
Com as constantes encontradas, podemos obter o número Biot para e na tabela 4-2 "coeficientes utilizados na solução aproximada do termo da condução de calor transiente unidimensional em paredes planas, cilindros e esferas".
Na tabela, vamos entrar que o número de Biot para e é .
Passo 6
Agora, podemos calcular o coeficiente de transferência de calor usando a seguinte relação:
Substituindo os valores conhecidos, temos:
Portanto, o coeficiente de transferência de calor é .
Passo 7
b) Podemos calcular a temperatura da superfície externa da costela quando estiver “mal passada” usando a seguinte relação:
Na superfície, temos que , assim, a equação fica:
Aqui é a temperatura na superfície da costela. Substituindo os dados conhecidos, temos:
Portanto, a temperatura da superfície externa da costela é .
Passo 8
c) Para calcular a quantidade de calor transferido para a costela, primeiro nós precisamos calcular a máxima transferência de calor possível com a seguinte equação:
Aqui é a máxima transferência de calor possível e é o calor específico da pressão constante. Substituindo pelos dados conhecidos, temos:
Agora, calculamos a quantidade de calor transferido para a costela com a seguinte expressão:
Aqui, é a quantidade real de calor transferido.
Substituindo pelos dados conhecido, temos:
Portanto, a quantidade real de transferência de calor é .
Passo 9
d) Para estimar o tempo necessário para assar a costela até estar “no ponto”, o que ocorre quando a parte interna da costela atinge a temperatura de , calculamos primeiro o número de Fourier na temperatura mais interna de utilizando a seguinte equação:
Substituindo pelos dados conhecidos, temos:
Passo 10
Podemos calcular o tempo apara que a costela fique bem passada usando a seguinte formula:
Isolando na equação.
Substituindo os valores.
Portanto, o tempo médio de cozimento para costela é .
Resposta
a)
b)
c)
d)