Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 20

Um fluido dielétrico a pressão atmosférica é aquecido com um fio horizontal de platina com diâmetro de 0,5   m m . Determine a temperatura do fio quando o fio é aquecido a 50 % do fluxo térmico crítico. As propriedades do fluido são   c p , l =   1300   J / ( k g · K ) ,   h f g = 142   k J / k g ,   k l   =   0,075   W / ( m   ·   K ) ,   v l   =   0,32   ×   10 – 6     m 2   / s ,   ρ l =   1400   k g / m 3   ,   ρ v   =   7,2   k g / m 3   ,   σ   =   12,4   ×   10 – 3   N / m ,   T s a t   =   34 ° C . Considere para as contantes da ebulição nucleada C s , f =   0,005   e   n   =   1,7 . Para cilindros horizontais pequenos, o fluxo térmico crítico é encontrado multiplicando-se o valor associado a um cilindro horizontal grande por um fator de correção F , sendo   F   =   0,89   +   2,27   e x p ( – 3,44 C o – 1 2 ) . O número de Confinamento é baseado no raio do cilindro e a faixa de aplicação do fator de correção é 1,3 ≤ C o ≤   6,7   [ 11 ] .

Passo 1

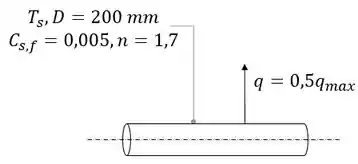
O que temos aqui?? Nos foi dado as (várias rs) propriedades do fluido dielétrico fervendo a 1   a t m em um fio de platina horizontal de 0,5   m m de diâmetro.

Além das constantes de ebulição de nucleados e o fator de correção para pequenos cilindros horizontais. Com isso, vamos encontrar a temperatura do fio quando aquecido a   50 % do fluxo de calor crítico.

Passo 2

Para resolver essa questão vamos assumir condições de estado estacionário. O fluxo crítico de calor para um cilindro horizontal grande, com C   =   0,1 31 , é:

q m a x ,   g r a n d e ' ' = C h f g ρ v σ g ρ l - ρ v ρ v 2 1 4

q m a x ,   g r a n d e ' ' = 0,1 31 ×   142 × 10 3 J k g × 7,2 k g m 3 12,4 × 10 - 3 N m × 9,8 m s 2 1 400 - 7,2 k g m 3 7,2 k g m 3 2 1 4

q m a x ,   g r a n d e ' ' = 180   k W m 2

O número do confinamento é dado por,

C o = σ g ρ l - ρ v R = 3,81

Que está na faixa de aplicabilidade da expressão para o fator de correção,   F ,

F   =   0,89   +   2,27 exp ⁡ – 3,44 3,81 – 1 2 = 1,28

Passo 3

A questão nos fala que o fio é operado a 50 % do fluxo de calor crítico, nós podemos escrever isso matematicamente da seguinte forma,

q s ' ' = 0,5 F q m a x ,   g r a n d e ' ' = 0,55 × 1,28 × 180   k W m 2 = 115 k W m 2

E o excesso de temperatura pode ser encontrado com a correlação de Rohsenow,

q s ' ' = μ l h f g g ρ l - ρ v σ 1 2 c p , l Δ T e C s , f h f g P r l   n 3 = 115 k W m 2

Substituindo os valores, temos,

115 × 10 3 W m 2 4,48 × 10 - 4 N . s m 2 × 142 × 10 3 J k g 9,8 m s 2 1 400 - 7,2 k g m 3 12,4 × 10 - 3 N m 1 2 1300 J k g . K × Δ T e 0,0 05 × 142 × 10 3 J k g 7,77 1 , 7 3            

Δ T e = 21,4 ° C

Então,

T s = 34 ° C + 21,4 ° C = 55,4 ° C

Resposta

T s = 55,4 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema de aquecimento geotérmico de um distrito envolve o transporte de água geotérmica a 110 ℃ ℃ a partir de um poço geotérmico para cidade com aproximadamente a mesma altitude e distância de 12k
Água a 1.800k g / h a 10 ℃ ℃ entra em um tubo liso de 10m m de diâmetro cuja temperatura da parede é mantida a 49 ℃ ℃. Calcule a o comprimento do tubo necessário para aquecer a água a 40 ℃ ℃ e b a tem
Repita o Prob. 8-87 considerando que uma camada de depósito mineral k = 3W / m ⋅ K de 0,25m m de espessura formou-se sobre a superfície interna do tubo.
Uma casa construída sobre a beira de um rio deve ser resfriada no verão com a utilização da água fria do rio que escoa a uma temperatura média de 15 ℃ ℃. Uma seção de 15m de comprimento de um tubo cir
Escoamentos internos forçados são chamados completamente desenvolvidos porque a ____ na seção transversal não muda mais na direção do escoamento.distribuição de temperatura;distribuição de entropia;di