Considere a fabricação de silício fotovoltaico, como descrito no Problema 1.42. A lâmina fina de silício é puxada do banho de silício fundido muito devagar e é submetida a uma temperatura ambiente de no interior da câmara de crescimento. Um coeficiente convectivo de está associado às superfícies expostas da lâmina de silício enquanto ela encontra-se dentro da câmara de crescimento. Calcule a velocidade máxima permitida da lâmina de silício, . O calor latente de fusão do silício é de . Pode-se considerar que a energia térmica liberada pela solidificação é removida por condução ao longo da lâmina.

A transferência de calor devido a solidificação é dada como:

A vazão mássica pode ser reescrita como:

Substituindo:

Para calcular a transferência de calor por condução nós precisamos considerar a placa de silício como sendo uma aleta infinita, ok?

Olhando a Tabela dada no livro:

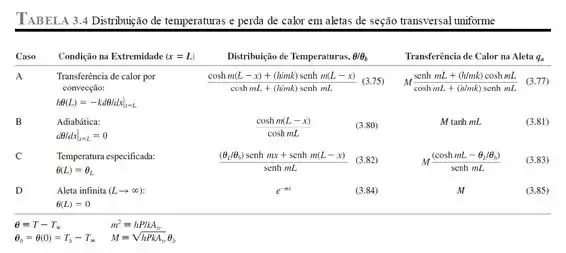
Quando fazemos o calor pode ser calculado como:

Como:

Então:

Na equação do Passo 1:

Agora que nós já sabemos como calcular a velocidade é só substituir os dados que já temos:

Ainda falta nós obtermos alguns dados, certo?

Para isso vamos olhar na Tabela A.1 para obter a temperatura de fusão do silício e a densidade:

Para achar a condutividade térmica nós precisamos da temperatura média da placa:

Para esta temperatura nós temos que:

Agora sim !!

Temos tudo o que precisamos, bora substituir?

Transformando:

Sendo assim, a placa de silício pode ser extraída do silicone fundido a uma velocidade de

Tranquilinha, não é?