Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 114

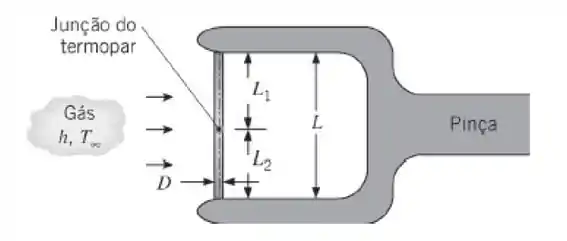
A temperatura de um gás escoando deve ser medida com uma junção de termopar em um fio esticado entre duas alças de uma pinça, um acessório de testes em túneis de vento. A junção é formada pela solda de topo de dois fios de diferentes materiais, como mostrado no esquema. Para fios com diâmetro D   =   125   m m e um coeficiente convectivo h   =   700 W m 2 K , determine a distância de separação mínima entre as duas alças da pinça, L = L1 + L2, para garantir que a temperatura da pinça não influencie a temperatura da junção e desta maneira, inviabilize a medida da temperatura do gás. Considere dois tipos diferentes de junções de termopares

constituídas de (i) fios de cobre e constantan, e (ii) fios de chroel e alumel. Avalie a condutividade térmica do cobre e do constantan a T = 300 K. Use k C h   =   19 W m K e k A l = 29 W m K para as condutividades térmicas dos fios de chromel e de alumel, respectivamente.

Passo 1

Mais uma bem legal ein galerinha !!

Para garantir que a temperatura da pinça não influencie a temperatura da junção nós precisamos que os dois fios se comportem como aletas infinitamente longas, ok?

Se é assim nós teremos que o comprimento dos fios deverão ser dados por:

L 1 ≥ 4,6 k C u A c h P 1 2

L 2 ≥ 4,6 k c o n A c h P 1 2

Vamos ver o que sabemos?

A área da seção transversal é dada por:

A c = π D 2 4

E o perímetro:

P = π D

Bora substituir?

L 1 ≥ 4,6 k C u π D 2 4 π D h 1 2 = 4,6 k C u D 4 h 1 2

L 2 ≥ 4,6 k c o n π D 2 4 π D h 1 2 = 4,6 k c o n D 4 h 1 2

O problema nos disse que:

d = 125   m m = 0,125   m

h = 700 W m 2 K

Como a temperatura é de 300 K nós podemos olhar na Tabela A.1 para achar as condutividades térmicas:

k C u = 401 W m K

k c o n = 23 W m K

Substituindo:

L 1 ≥ 4,6 401 W m K 0,125   m 4 700 W m 2 K 1 2 = 0,615   m

L 2 ≥ 4,6 23 W m K 0,125   m 4 700 W m 2 K 1 2 = 0,147   m

Analisando o comprimento total:

L ≥ L 1 + L 2 = 0,615   m + 0,147   m = 0,762   m

Portanto, a separação entre as duas alças da pinça para que a temperatura da pinça não influencie na temperatura da junção deve ser no mínimo de 0,762   m .

Passo 2

Agora, quando a junção é feita de chroel e alumel, teremos:

k C h   =   19 W m K

k A l = 29 W m K

Então os novos comprimentos serão:

L 1 ≥ 4,6 k C h D 4 h 1 2

L 2 ≥ 4,6 k a l D 4 h 1 2

Substituindo:

L 1 ≥ 4,6 19 W m K 0,125   m 4 700 W m 2 K 1 2 = 0,134   m

L 2 ≥ 4,6 29 W m K 0,125   m 4 700 W m 2 K 1 2 = 0,166   m

Analisando o comprimento total:

L ≥ L 1 + L 2 = 0,134   m + 0,166   m = 0,3   m

Portanto, a separação entre as duas alças da pinça para que a temperatura da pinça não influencie na temperatura da junção deve ser no mínimo de 0,3   m .

Muito menor do que a primeira opção, não é?!

E finalizamos mais umaa !!

Resposta

i           0,762   m ;

i i         0,300   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Problema 3-80E. Usando o software EES (ou outro programa), investigue os efeitos da condutividade térmica do material do tubo e do diâmetro externo do tubo no comprimento do tubo necessá
Na indústria farmacêutica, um tubo de cobre k = 400 W m·K com diâmetro interno de 20 mm e espessura de parede de 2,5 mm é usado para transportar oxigênio líquido para um tanque de armazenamento. O oxi
A taxa de transferência de calor da parede de um tubo circular com convecção agindo sobre a superfície externa é dada, por unidade de seu comprimento, q ˙ = 2 π L T i - T o ln ⁡ r o / r i k + 1 r o h
Um tanque de armazenamento de oxigênio líquido de hospital de 1m de diâmetro mantém o oxigênio líquido a 90K . O reservatório é constituído por uma casca de alumínio k = 170W / m ⋅ K de 0,5c m de espe
Um tanque de armazenamento de oxigênio líquido de hospital de 1m de diâmetro interno mantém o oxigênio líquido a 90K . O reservatório é constituído por uma casca de alumínio k = 170W / m ⋅ K de 0,5c m