Considere uma janela de vidro 1,5 m de altura, 2,4 m de largura, espessura de 6 mm e condutividade térmica . Determine a taxa de transferência de calor permanente através dessa janela de vidro e a temperatura de sua superfície interna quando o quarto é mantido a 24 °C, enquanto a temperatura externa é -5 °C. Considere os coeficientes de transferência de calor por convecção sobre as superfícies interna e externa da janela iguais a e . Ignore qualquer transferência de calor por radiação.

Nosso ponto de partida é colocar as hipóteses do nosso problema. São elas que possibilitam a sua solução!

Portanto, temos um problema de transferência de calor em regime permanente, unidimensional e condutividade térmica constante.

Podemos associar este problema a noção de resistências elétricas. O calor fluirá da superfície interna para a superfície interna, devido ao gradiente de temperaturas. Portanto, temos três elementos no nosso circuito: uma resistência de convecção da superfície interna para o vidro; a própria condução no vidro; e a convecção na superfície externa.

Podemos representar esta situação através da seguinte figura:

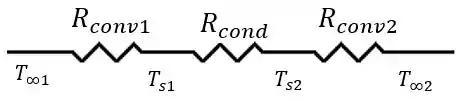
Calculando as resistências térmicas, temos:

Agora, basta aplicarmos as fórmulas da condução para obtermos tanto a taxa de transferência de calor quanto a temperatura da superfície interna do vidro.