Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 24

24 – Considere um meio cuja equação de condução de calor na forma mais simples é

∂ 2 T ��� x 2 + ∂ 2 T ∂ y 2 = 1 ∝ ∂ T ∂ t

  1. A transferência de calor é permanente ou transiente?
  2. A transferência de calor é uni, bi ou tridimensional?
  3. Há geração de calor no meio?
  4. A condutividade térmica do meio é constante ou variável?

Passo 1

  1. Se observamos a equação, vamos perceber que a temperatura depende do tempo t , logo:

    2. ∂ T ∂ t ≠ 0

    Portanto, isso implica que o processo é instável, já que o tempo deve ser diferente de zero, assim, a transferência de calor por condução é transitória.

    Passo 2

  2. ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 = 1 ∝ ∂ T ∂ t

    A partir da equação fornecida, percebe-se que temos variação no eixo x   e   y . Portanto, a transferência de calor é bidimensional.

    Passo 3

  3. A partir da equação de condução de calor, notamos que não há geração de calor devido à

    4. e ˙ g e r a d o k = 0

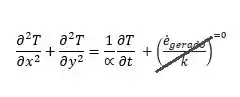
    Portanto, não há geração de calor no meio.

    Passo 4

  4. A expressão para difusividade térmica é

∝ = k ρ c p

Onde:

k é a condutividade térmica.

p é a densidade.

c p é o calor específico.

Substituindo essa expressão na equação de condução de calor, temos:

∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 = ρ c p k ∂ T ∂ t

Aqui, a condutividade térmica não depende da temperatura. Portanto, a condutividade térmica do meio é constante.

Resposta

  1. Transitória
  2. Bidimensional
  3. Não
  4. Constante
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

78 – Uma barra de combustível nuclear cilíndrica de 1c m de diâmetro é inserida em um tubo concêntrico de 2c m de diâmetro, onde a água de resfriamento escoa na região anular entre a barra de combustí
81 – Considere um extenso sólido de formato cilíndrico com raio r 0 = 4c m e condutividade térmica k = 25 W m ⋅ K . Calor é gerado uniformemente no cilindro a uma taxa de e g e r = 35W / c m 3 . A sup
76 – Considere uma extensa placa de latão de 5c m de espessira k = 111 W m ⋅ K na qual calor é gerado uniformemente a uma taxa de 2 × 10 5W / m 3 . Um lado da placa é isolado, enquanto o outro é expos
77 – Reconsidere o Prob, 2-76. Usando EES (ou outro programa), analise o efeito do coeficiente de transferência de calor nas temperaturas máxima e mínima da placa. Varie o coeficiente de transferência
Calor é gerado uniformemente a uma taxa de 4,2 ⋅ 10 6W / m 3 em uma esfera ( k = 45W / m ⋅ K ) com 24 cm de diâmetro. A esfera é exposta à água fria a 0 °C com coeficiente de transferência de calor de