Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 77
77 – Reconsidere o Prob, 2-76. Usando EES (ou outro programa), analise o efeito do coeficiente de transferência de calor nas temperaturas máxima e mínima da placa. Varie o coeficiente de transferência de calor de a . Trace as temperaturas máxima e mínima como função do coeficiente de transferência de calor e discuta os resultados obtidos.
Passo 1
A temperatura máxima é obtida no ponto de centro da parede do avião no caso de parede plana cuja espessura de 2 L . Em seguida, se se considerar a espessura da placa de L isolados de um lado e expostos ao ambiente no outro lado é equivalente à metade de parede plana cuja espessura é de 2 L .
Como a placa é isolada em um lado da placa e o outro lado da placa é exposto à atmosfera, a temperatura mais alta ocorrerá na superfície isolada da placa e a temperatura mais baixa ocorrerá no outro lado da placa.
Passo 2
Encontre a temperatura mais baixa da placa usando a seguinte equação:
Aqui, é a temperatura do ambiente, é a quantidade de geração de calor, é a espessura da placa e é a temperatura mais baixa da placa.
Transforme os valores do enunciado para o sistema internacional . Em seguida, substituía na equação:
Passo 3
Escrever a equação no EES e variar o valor de entre a , e determinar a temperatura mais baixa na parede para os valores do coeficiente de transferência de calor.
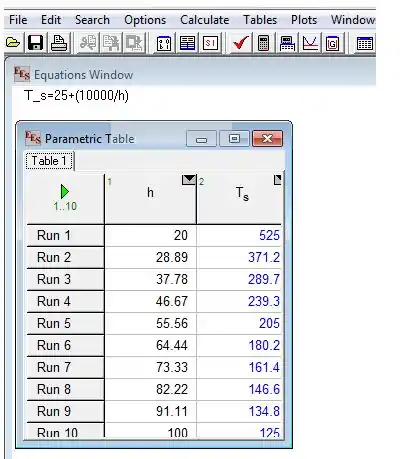
Passo 4
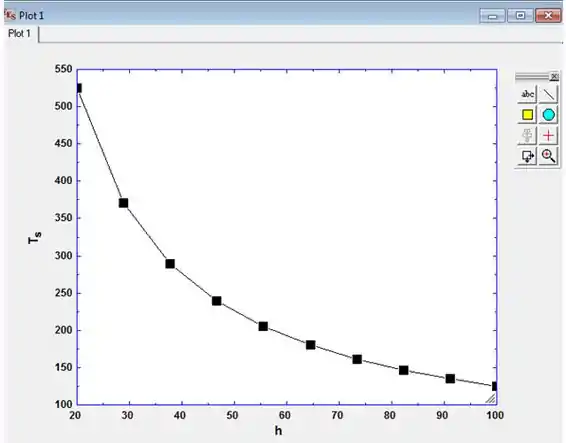
Use a opção “Plot” e desenhe a curva, representando a temperatura mínima, em função do coeficiente de transferência de calor, .
Passo 5
Calcule a temperatura mais alta na superfície isolada.
Aqui, é a condutividade térmica da placa de latão, é a temperatura mais alta da superfície isolada.
Transforme os valores do enunciado para o sistema internacional . Em seguida, substituía na equação:
Temos que,
Passo 6
Escrever a equação no EES e variar o valor de entre a , e determinar a temperatura mais alta na parede para os valores do coeficiente de transferência de calor correspondente usando a opção “quadros”.
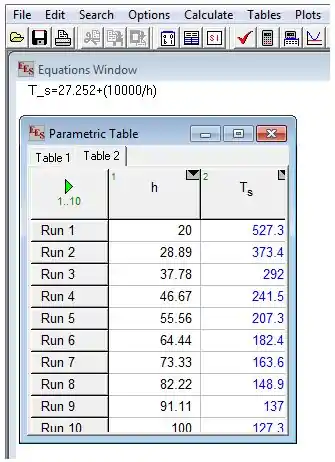
Passo 7
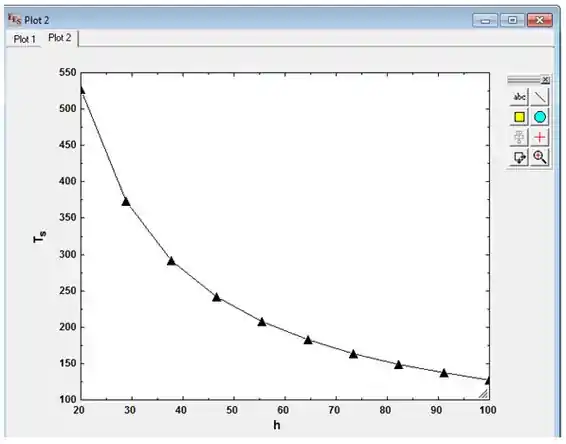
Use a opção “Plot” e desenhe a curva, representando a temperatura máxima, em função do coeficiente de transferência de calor,.
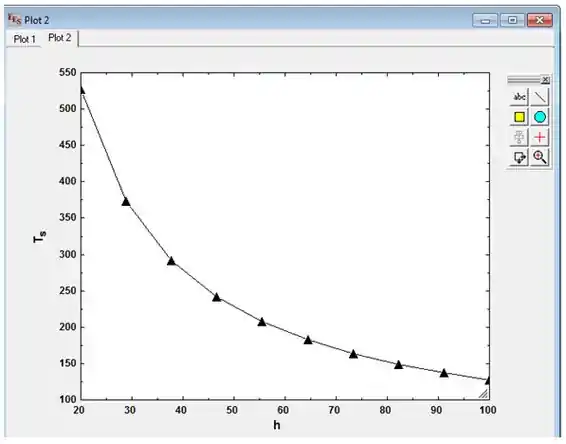
Resposta
