Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 92
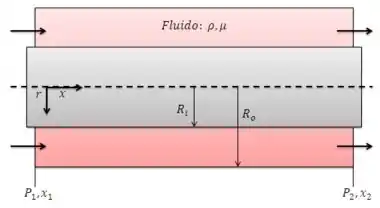
Considere novamente o tubo anular representado na Figura . Suponha que a pressão seja constante em todos os pontos (não há gradiente de pressão empurrando o escoamento). Porém, suponha que a parede interna esteja se movendo a uma velocidade constante para a direita. A parede externa ainda está estacionária. (Esse é um tipo de escoamento de Couette axis-simétrico). Encontre uma expressão para a componente de velocidade em função de e de outros parâmetros do Problema.
Passo 1
Para começar, vamos retomar qual é a situação apresentada na Figura . Tínhamos um líquido com propriedades constantes () escoando no espaço entre dois cilindros.
Os dois cilindros eram fixos e o escoamento ocorria devido à existência de um diferencial de pressão constante ao longo da tubulação. Tudo bem até aqui?
Agora, o exercício propõe uma nova situação em que não há mais o diferencial de pressão e, que o escoamento ocorre devido à movimentação do cilindro interno com velocidade constante. Ou seja, a situação que vamos trabalhar é:
Vamos lá?
Passo 2
O primeiro passo para chegarmos ao perfil de velocidades é a aplicação da equação da continuidade para coordenadas cilíndricas:
Assumindo que estamos em um processo estacionário e, que apenas a componente da velocidade é não-nula:
Então, a equação da continuidade é reduzida à :
Podemos concluir então que a velocidade não depende da direção . Ou seja:
Nosso próximo passo para obter o perfil de velocidade será aplicar a equação de Navier-Stokes.
Passo 3
Como o escoamento só ocorre na direção , vamos aplicar a equação de Navier-Stokes para esta componente:
Vamos agora olhar os termos do lado esquerdo da equação.
Sabemos que o processo ocorre em regime permanente. Além disso, as componentes de velocidade e são nulas e, pela equação da continuidade vimos que . Então,
Então, o lado esquerdo da equação se reduz à:
Vamos agora verificar os termos do lado direito.
Para esta situação, a pressão é constante em todos os pontos da tubulação. Além disso, não temos ação da força gravitacional e, vale relembrar que . Assim:
E a equação de Navier-Stokes fica:
Passo 4
Como a derivada em relação à é nula podemos dizer que:
Em que é uma constante. Continuando:
Integrando os dois lados da equação em relação à :
Para obter as constantes e vamos aplicar as condições de contorno para o problema. Pelo princípio da aderência sabemos que . Então, nossas condições de contorno são:
Passo 5
Aplicando estes valores no perfil de velocidades ficamos com:
Subtraindo a primeira equação da segunda:
Substituindo na primeira relação:
Se aplicarmos as constantes no perfil de velocidade ficaremos com:
Resposta
O perfil de velocidades para este caso é :