Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 91

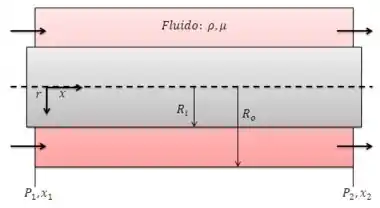
Considere o escoamento permanente, incompressível, laminar de um fluido newtoniano em um escoamento anular redondo infinitamente longo com raio interno R i e raio externo R o . Ignore os efeitos da gravidade. É aplicado um gradiente constante negativo de pressão ∂ P / ∂ x na direção x , ∂ P ∂ x = P 2 - P 1 x 2 - x 1 , onde x 1 e x 2 são duas localizações arbitrárias ao longo do eixo x , e P 1 e P 2 são as pressões naquelas duas localizações. O gradiente de pressão pode ser causado por uma bomba e/ou gravidade. Note que aqui adotamos um sistema de coordenadas cilíndricas modificado com x em lugar de z para a componente axial, ou seja, ( r ,   θ ,   x ) e ( u r ,   u θ ,   u ) . Deduza uma expressão para o campo de velocidade no espaço anular do tubo.

Passo 1

Temos a seguinte situação: um fluido com propriedades constantes ( ρ ,   μ ) escoa no espaço anular entre dois cilindros fixos. O escoamento ocorre devido ao gradiente de pressão na direção x .

Nossa tarefa será determinar qual é o perfil de velocidades para esta situação. Vamos lá?

Para começar, nosso primeiro passo para obter o perfil será aplicar a equação da continuidade para coordenadas cilíndricas:

∂ ρ ∂ t + 1 r ∂ ∂ r r ρ u r + 1 r ∂ ∂ θ ρ u θ + ∂ ∂ x ρ u = 0

Considerando que o processo ocorre em regime permanente e que apenas a componente u da velocidade é não-nula:

∂ ρ ∂ t = 0 ;

u r = 0 → 1 r ∂ ∂ r r ρ u r = 0 ;

u θ = 0 → 1 r ∂ ∂ θ ρ u θ = 0

Então, a equação da continuidade é reduzida à:

∂ ∂ x ρ u = 0

ρ ∂ ∂ x u = 0

∂ u ∂ x = 0

Concluímos então que a velocidade u não depende da direção x . Ou seja:

u = u ( r )

Passo 2

Nosso próximo passo para obter o perfil de velocidades será aplicar a equação de Navier-Stokes. Como o escoamento ocorre apenas na direção x , vamos aplicar a equação de Navier-Stokes para esta componente:

ρ ∂ u ∂ t + u r ∂ u ∂ r + u θ r ∂ u ∂ θ + u ∂ u ∂ x = - ∂ P ∂ x + ρ g x + μ 1 r ∂ ∂ r r ∂ u ∂ r + 1 r 2 ∂ 2 u ∂ θ 2 + ∂ 2 u ∂ x 2

Vamos começar analisando o lado esquerdo da equação.

Estamos em regime permanente e as componentes da velocidade u r e u θ são nulas. Além disso, vimos pela equação da continuidade que u = u ( r ) . Então:

∂ u ∂ t = 0 ;

u r = 0 ;

u θ = 0 ;

∂ u ∂ x = 0

Assim, o lado esquerdo da equação é reduzido à:

ρ 0 + 0 × ∂ u ∂ r + 0 × ∂ u ∂ θ + u × 0 = 0

Vamos agora olhar para os termos do lado direito.

Pelo enunciado, a ação da força gravitacional pode ser desprezada. Além disso, como acabamos de ver u = u ( r ) . Portanto:

ρ g x = 0 ;

∂ 2 u ∂ θ 2 = 0 ;

∂ 2 u ∂ x 2 = 0

Nossa equação fica:

0 = - ∂ P ∂ x + 0 + μ 1 r ∂ ∂ r r ∂ u ∂ r + 1 r 2 × 0 + 0

0 = - ∂ P ∂ x + μ 1 r ∂ ∂ r r ∂ u ∂ r

Temos um gradiente de pressão constante, então:

∂ P ∂ x = P 2 - P 1 x 2 - x 1

Substituindo na equação de Navier-Stokes:

P 2 - P 1 x 2 - x 1 = μ 1 r ∂ ∂ r r ∂ u ∂ r

Passo 3

Para continuar a obtenção do perfil, vamos rearranjar a equação:

P 2 - P 1 x 2 - x 1 = μ 1 r ∂ ∂ r r ∂ u ∂ r

P 2 - P 1 r μ x 2 - x 1 = ∂ ∂ r r ∂ u ∂ r

Integrando os dois lados em relação à ∂ r :

∫ ∂ ∂ r r ∂ u ∂ r ∂ r = ∫ P 2 - P 1 r μ x 2 - x 1 ∂ r

r ∂ u ∂ r = P 2 - P 1 r 2 2 μ x 2 - x 1 + C 1

∂ u ∂ r = P 2 - P 1 r 2 μ x 2 - x 1 + C 1 r

Se fizermos uma nova integração com relação à ∂ r ficamos com:

∫ ∂ u ∂ r ∂ r = ∫ P 2 - P 1 r 2 μ x 2 - x 1 + C 1 r ∂ r

u = P 2 - P 1 r 2 4 μ x 2 - x 1 + C 1 ln ⁡ r + C 2

Vamos agora aplicar as condições de contorno ao perfil para obter as constantes C 1 e C 2 . Pelo princípio da aderência as condições de contorno são:

u r = R i = 0

u r = R o = 0

Já que os cilindros são fixos.

Passo 4

Aplicando estas duas condições:

0 = P 2 - P 1 R i 2 4 μ x 2 - x 1 + C 1 ln ⁡ R i + C 2

0 = P 2 - P 1 R o 2 4 μ x 2 - x 1 + C 1 ln ⁡ R o + C 2

Subtraindo a primeira equação da segunda:

0 = P 2 - P 1 4 μ x 2 - x 1 ( R o 2 - R i 2 ) + C 1 ( ln ⁡ R o - ln ⁡ R i )

- P 2 - P 1 4 μ x 2 - x 1 ( R o 2 - R i 2 ) = C 1 ( ln ⁡ R o R i   )

C 1 = - P 2 - P 1 4 μ x 2 - x 1 × ( R o 2 - R i 2 ) ln ⁡ R o R i

Substituindo C 1 na primeira relação:

0 = P 2 - P 1 R i 2 4 μ x 2 - x 1 - P 2 - P 1 4 μ x 2 - x 1 × ( R o 2 - R i 2 ) ln ⁡ R o R i × ln ⁡ R i + C 2

C 2 = P 2 - P 1 4 μ x 2 - x 1 × R o 2 - R i 2 ln ⁡ R o R i × ln ⁡ R i - R i 2

Aplicando as duas condições de contorno no perfil de velocidade ficamos com:

u = P 2 - P 1 r 2 4 μ x 2 - x 1 - P 2 - P 1 4 μ x 2 - x 1 × ( R o 2 - R i 2 ) ln ⁡ R o R i × ln ⁡ r + P 2 - P 1 4 μ x 2 - x 1 × R o 2 - R i 2 ln ⁡ R o R i × ln ⁡ R i - R i 2

u = P 2 - P 1 4 μ x 2 - x 1 × r 2 - R o 2 - R i 2 ln ⁡ R o R i × ln ⁡ r - R i 2 + R o 2 - R i 2 ln ⁡ R o R i × ln ⁡ R i

u = P 2 - P 1 × R o 2 - R i 2 4 μ x 2 - x 1 × r 2 - R i 2 R o 2 - R i 2 - ln ⁡ r ln ⁡ R o R i + ln ⁡ R i ln ⁡ R o R i

u = P 2 - P 1 × R o 2 - R i 2 4 μ x 2 - x 1 × r 2 - R i 2 R o 2 - R i 2 + ln ⁡ R i r ln ⁡ R o R i

Resposta

O perfil de velocidade no espaço anular é:

u = P 2 - P 1 × R o 2 - R i 2 4 μ x 2 - x 1 × r 2 - R i 2 R o 2 - R i 2 + ln ⁡ R i r ln ⁡ R o R i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A regra do produto pode ser aplicada ao divergente do escalar f vezes o vetor G → como: ∇ → . f G → = G → . ∇ → f + f ∇ → . G → . Expanda ambos os lados desta equação em coordenadas cartesianas e veri
O produto exterior de dois vetores é um tensor de segunda ordem com nove componentes. Em coordenadas cartesianas, ele é:A regra do produto aplicada à divergência do produto aplicada ao divergente de d
Seja o vetor G → ser dado por G → = 4 x z i → - y 2 j → + y z k → e seja V o volume de um cubo de aresta unitária com seu vértice na origem, limitado por x = 0 a 1, y =0 a 1 e z = 0 a 1 (Fig. P9–9). A
Neste capítulo nós deduzimos a equação de continuidade de duas maneiras: usando o teorema da divergência e somando as vazões em massa através de cada face de um volume de controle infinitesimal. Expli
Se um campo de escoamento é compressível, o que podemos dizer sobre a derivada material da densidade? E se o campo de escoamento for incompressível?