Analise e discuta dois casos limites do Problema .
(a) O espaçamento é muito pequeno. Mostre que o perfil de velocidade se aproxima de uma função linear da parede do cilindro externo até a parede do cilindro interno. Em outras palavras, para um espaçamento muito pequeno o perfil de velocidade se reduz àquele de um escoamento Couette simples bidimensional.
(b) O raio do cilindro externo se torna infinito enquanto o raio do cilindro interno se torna muito pequeno. Isso é uma aproximação de que tipo de escoamento?
Passo 1
Vamos começar relembrando alguns pontos do Problema . A situação apresentada neste problema era a seguinte:
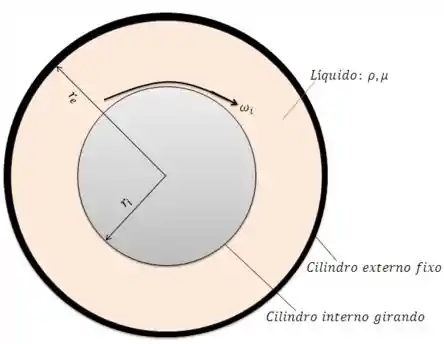
Temos um líquido com propriedades constantes () confinado no espaço entre dois cilindros concêntricos. O cilindro externo gira com uma velocidade angular , enquanto o cilindro externo encontra-se parado. Tudo bem até aqui?
Agora que retomamos o princípio do Problema podemos começar este exercício. No item (a), devemos considerar uma condição limite em que o espaçamento entre os cilindros é muito pequeno. Ou seja, algo assim:
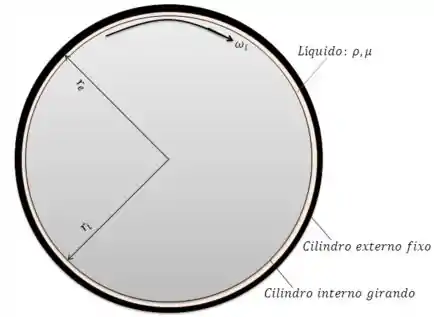
Vamos ver como será o perfil de velocidade para este caso.
Passo 2
Para começar, vamos dar um zoom na figura e adicionar o nosso eixo de coordenadas:
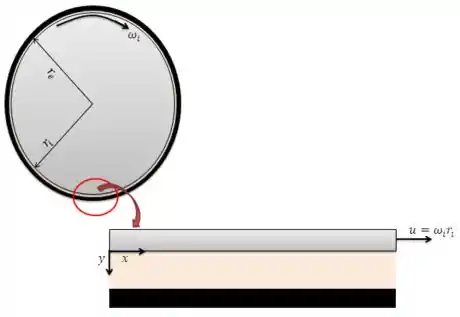
Espera...isso lembra alguma coisa?
Exatamente!!! Nesta condição limite o que acontece é que o espaço entre os cilindros é tão pequeno que podemos desprezar o efeito da curvatura e aproximar nosso problema para um escoamento Couette entre duas placas planas. Tudo bem até aqui?
Vamos agora partir para a determinação do perfil de velocidade. Para isso, começamos com a equação da continuidade para coordenadas cartesianas:
Assumindo que estamos na condição de regime permanente e que as velocidades nas direções e são nulas:
Então, nossa equação se reduz à:
Ou seja, a velocidade não depende de . O que é equivalente dizer que:
Nosso próximo passo para obter o perfil de velocidade será aplicar a equação de Navier-Stokes. Vamos lá?
Passo 3
Como o fluido só está escoando na direção vamos aplicar a equação de Navier-Stokes para a componente . Ela é dada por:
Como estamos em um processo estacionário, e são nulas e , os termos do lado esquerdo da equação são:
Ou seja,
Vamos agora olhar para o lado direito da equação. O fluido escoa apenas devido à movimentação da placa (cilindro) superior, sem sofrer ação de um diferencial de pressão ou da força gravitacional. Então:
Além disso, vimos pela equação da continuidade que , ou seja,
Nossa equação se reduz à:
Passo 4
Se a segunda derivada de em relação à é zero, isso implica que:
Em que é uma constante. Integrando em relação à :
Já podemos ver que o perfil de velocidade é uma função linear, assim como foi dito no enunciado. Mas, para finalizar vamos aplicar as condições de contorno para a velocidade para obter e . As condições de contorno são:
Sendo que é o espaçamento entre os cilindros.
Aplicando estas condições ficamos com:
Substituindo as constantes no perfil:
Passo 5
Vamos agora para o item (b). Neste item, o que acontece é que agora o cilindro externo é muito maior que o interno, ou seja, o espaçamento tende a infinito. Vamos ver o que acontece nesse caso:
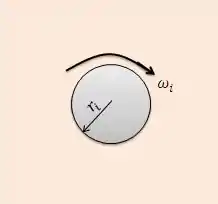
Neste caso, o cilindro externo está tão afastado que podemos desprezar seu efeito no perfil de escoamento. Nesta situação limite o cilindro interno é a única geometria relevante para a deformação do fluido, de forma que podemos considerar que o fluido apenas escoa na superfície exterior de um cilindro, ao invés de estar em um espaço anular.
Este tipo de aproximação chamamos de escoamento externo. A principal diferença entre esta situação e as propostas no item (a) e no Problema é que, apesar de haver dissipação de energia até que a velocidade do fluido atinja , isto ocorrerá devido ao atrito entre as camadas de fluido e não mais pela presença da segunda geometria (, pelo princípio da aderência).
Resposta
(a) Demonstração.
(b) Para esta situação limite podemos aproximar o escoamento para um escoamento externo sobre a superfície de um cilindro.