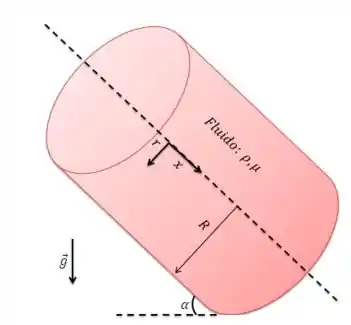
Considere um escoamento permanente, incompressível, laminar de um fluido newtoniano em um tubo redondo infinitamente longo de diâmetro ou raio inclinado de um ângulo (Figura ). Não há gradiente de pressão aplicado (). Em vez disso, o fluido escoa pelo tubo somente devido à gravidade. Adotamos o sistema de coordenadas mostrado, com paralelo ao eixo do tubo. Deduza uma expressão para a componente de velocidade como uma função de raio e dos outros parâmetros do problema. Calcule a vazão em volume e a velocidade axial média através do tubo.

Nosso próximo passo para obter o perfil de velocidades será aplicar a equação de Navier-Stokes. Como só temos velocidade na componente , vamos usar a equação de Navier-Stokes para esta direção:

Vamos analisar primeiro os termos do lado esquerdo.

Temos um escoamento em regime estacionário e, como mencionamos anteriormente as componentes de velocidade e são nulas. Além disso, pela equação da continuidade vimos que . Então:

Assim, o lado esquerdo se reduz à:

Vamos agora olhar para os termos do lado direito.

Não temos gradiente de pressão no escoamento e, na direção , temos uma componente da força gravitacional. Também, vamos utilizar o resultado da equação de continuidade :

A equação de Navier-Stokes fica:

Para continuar, vamos integrar os dois lados da equação em relação à :

Para encontrar , já vamos aplicar a primeira condição de contorno. Considerando que temos um perfil simétrico devemos ter velocidade máxima no centro. Tudo bem?

Então

Portanto, ficamos com:

Integrando novamente em relação à :

Para obter a constante vamos aplicar a segunda condição de contorno. Pelo princípio da aderência:

Aplicando esta condição:

Substituindo nosso perfil de velocidades é:

Agora que temos o perfil vamos calcular qual é a vazão volumétrica de fluido. Para isso, vamos aplicar a seguinte relação:

Para finalizar, vamos encontrar a velocidade média através da equação: