Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 141
Uma parede plana de espessura 2L = 50 mm e condutividade térmica constante gera calor uniformemente a uma taxa de . Sob condições permanentes, a distribuição de temperatura na parede tem a forma , onde e , com em metros. A origem da coordenada encontra-se no ponto médio da parede.
- Determine as temperaturas das superfícies e esboce a distribuição de temperatura da parede.
- Qual é a taxa volumétrica de geração de calor ?
- Determine os fluxos de calor das superfícies e .
- Qual é a relação entre esses fluxos, a taxa de geração de calor e a geometria da parede?
Passo 1
O nosso primeiro passo é fazer considerações para resolver o nosso problema. Sendo assim, temos um problema de regime permanente, com condução de calor unidimensional, geração de calor, condutividade térmica constante.
Nosso primeiro passo é determinarmos as temperaturas das superfícies e esboçar a distribuição de temperaturas da parede.
Como a função temperatura já nos foi dada, basta substituirmos os valores de relativos as superfícies. Como a função está centrada no ponto médio da parede, então, as coordenadas das superfícies são e . Desta forma, temos:
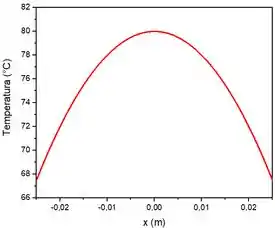
Portanto, ambas as superfícies possuem a mesma temperatura. Esboçando a distribuição de temperaturas, temos:
Passo 2
Agora, vamos determinar o termo de geração de calor . Para isto, precisamos relembrar qual é a EDO que representa a condução de calor no nosso sólido.
Devido a todas as condições discutidas no início do Passo 1, esta EDO é:
E agora? O que devemos fazer??? Bom, percebam que nós já temos a função temperatura! Então, basta derivarmos ela duas, e assim obteremos o termo de geração! Logo,
E assim resolvemos a letra b).
Passo 3
Agora vamos calcular os fluxos de calor nas superfícies. Pela lei de Fourier, sabemos que o fluxo é dado por:
Portanto, na superfície , temos:
Já na superfície , temos:
E assim finalizamos a letra c).
Passo 4
Para finalizarmos a questão, basta escrevermos a relação entre os fluxos, o termo de geração de calor e a geometria do sólido.
E aí fica o questionamento: como encontramos esta relação? A resposta é mais simples do que parece. Basta fazermos um balanço de energia no sólido. Com isto, teremos:
A energia que sai é o produto dos fluxos pelas áreas de superfície. Já a energia gerada é o produto de pelo volume do sólido. Portanto,
E assim encontramos a relação que a questão nos pede!
Resposta
- A temperatura das superfícies e a distribuição de temperaturas na parede são:
- A taxa volumétrica de geração de calor é dada por:
- Os fluxos de calor nas superfícies são:
- A relação entre os termos é:
