Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 63
63 - Considere um pino (aleta) horizontal com de diâmetro e de comprimento fabricado em aço-carbono não ligado . A base do pino é mantida a , enquanto o ar ambiente quiescente e a vizinhança estão a . Considere a extremidade do pino adiabática.
(a) Estime a taxa de transferência de calor no pino, . Use uma temperatura média para a superfície do pino de ao avaliar o coeficiente de transferência de calor por convecção natural e o coeficiente de transferência por radiação linearizado. Qual é a sensibilidade dessa estimativa em relação à sua escolha da temperatura média para a superfície do pino?
(b) Use o método de diferenças finitas para obter com os coeficientes de transferência de calor por convecção e por radiação com base nas temperaturas locais no pino, ao invés da temperatura média. Como seu resultado se compara ao da solução analítica obtido na parte (a)?
Passo 1
Considere a seguinte figura mostrando a aleta:
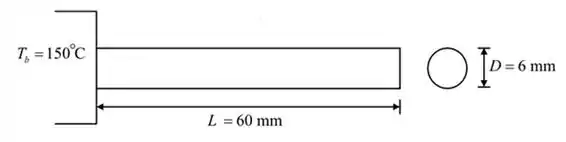
Passo 2
Como dito na letra (a), usaremos a temperatura de para superfície.
Portanto, a temperatura de filme é:
Portanto, obtenha as propriedades do ar à temperatura de .
Viscosidade cinemática é:
Condutividade térmica é:
A difusividade térmica é:
O número Prandtl é:
O Coeficiente de expansão é:
Passo 3
O número Rayleigh pode ser calculado com a seguinte relação:
Substituindo pelos valores conhecidos, temos:
Temos que a taxa de calor para a aleta do pino com uma ponta adiabática é dada por:
Onde:
Passo 4
Vamos começar então, calculando o número de Nusselt para depois encontrar o coeficiente convectivo.
Passo 5
Agora precisamos calcular os dois coeficientes convectivos para obter o .
Aqui, é a temperatura da superfície, é a emissividade, é a constante de Stefan-Boltzmann e é a temperatura ambiente.
Agora que temos ambas, podemos calcular a total:
Passo 6
Temos agora como achar a taxa de calor para a aleta do pino com uma ponta adiabática, basta substituir pelos valores conhecidos.
Logo, temos que:
Passo 7
Usando a mesma análise feita anteriormente, temos que o método de diferenças finitas para superfícies estendidas fornece os seguintes resultados:
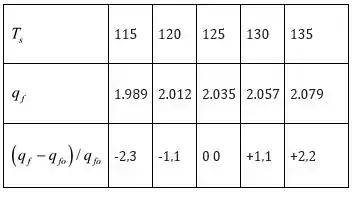
A partir dos valores acima, observa-se que a aleta não é muito sensível à variação em .
Resposta
- Pergunte a um especialista.