4 - Estime o coeficiente de transferência de calor, , associado aos pontos na Figura 10.4. Qual ponto está associado ao maior valor de ? Qual ponto está associado ao menor valor de ? Determine a espessura da manta de vapor no ponto de Leidenfrost, desprezando a transferência de calor por radiação através da manta. Admita que o sólido é uma superfície plana.

Na figura 10.4 (Curva de ebulição típica para água a ), o excesso de temperatura e fluxo de calor no ponto B é o seguinte:

Substituindo esses valores na equação , temos:

Na figura 10.4 (Curva de ebulição típica para água a ), o excesso de temperatura e fluxo de calor no ponto C é o seguinte:

Substituindo esses valores na equação , temos:

Na figura 10.4 (Curva de ebulição típica para água a ), o excesso de temperatura e fluxo de calor no ponto D é o seguinte:

Substituindo esses valores na equação , temos:

Na figura 10.4 (Curva de ebulição típica para água a ), a temperatura excessiva e o fluxo de calor no ponto E são os seguintes:

Substituindo esses valores na equação , temos:

Agora vamos tabular o excesso de temperatura, fluxo de calor e coeficientes locais de transferência de calor nos pontos B, C, D e E.

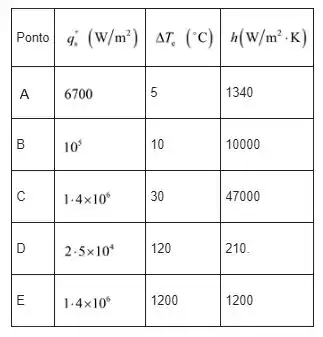
Entre estes, o maior coeficiente de transferência de calor ocorre no ponto C, correspondendo ao fluxo crítico de calor.

O menor coeficiente de transferência de calor ocorre no ponto D, o ponto de geada de Leiden.

No ponto de geada de Leiden, se a radiação é negligenciada, a transferência de calor é devida exclusivamente à condução através do filme de vapor. O ponto D é o ponto de geada de Leiden. A espessura da manta de vapor calculada no ponto D.

Vamos calcular a espessura da manta de vapor no ponto de geada de Leiden pela seguinte fórmula:

Assim, a espessura da manta de vapor no ponto de geada de Leiden é .