Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 116

Painéis quadrados ( 250   m m × 250   m m ) com um acabamento plástico decorativo de elevada refletividade são curados em um forno a 125 ° C e resfriados em ar quiescente a 29 ° C . Considerações de qualidade ditam que os painéis devam permanecer na posição horizontal e que a taxa de resfriamento deva ser controlada. Para aumentar a produtividade da fábrica, propõe-se substituir o método de resfriamento em batelada por um sistema de correia transportada com uma velocidade de 0,5   m / s .

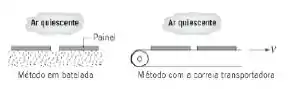
Compare as taxas iniciais (imediatamente após deixar o forno) de transferência de calor por convecção nos dois métodos de resfriamento.

Passo 1

Começamos o problema calculando a temperatura de filme:

T f = T s + T ∞ 2

Dados:

T s = 125 ° C ;

T ∞ = 29 ° C .

Temos:

T f = 125 + 29 2

T f = 77 ° C = 350   K

Pela Tabela A .   4 obtemos as seguintes propriedades para o ar sob a temperatura de 350   K :

v = 20,92 × 10 - 6   m 2 / s

k = 0,030   W / m ⋅ K

α = 29,9 × 10 - 6   m / s 2

P r = 0,700

β = 1 T f = 1 350 = 2,86 × 10 - 3   K - 1

Passo 2

Calculando G r L R e L 2 , sendo as equações de G r L e R e L dadas por:

G r L = g β T s - T ∞ L 3 v 2   e   R e L = u ∞ L v

Dados:

g = 9,8   m / s 2 ;

L = 0,250   m ;

u ∞ = 0,5   m / s .

Temos:

G r L = 9,8 ⋅ 2,86 × 10 - 3 ⋅ 125 - 29 ⋅ 0,250 3 ( 20,92 × 10 - 6 ) 2

G r L = 9,60 × 10 7

R e L = 0,5 ⋅ 0,250 20,92 × 10 - 6

R e L = 5,98 × 10 3

Desse modo:

G r L R e L 2 = 9,60 × 10 7 5,98 × 10 3 2

G r L R e L 2 = 2,68

Passo 3

Para placa estacionária:

R a L = G r L = 9,60 × 10 7

Pela Eq . 9.31:

N u ¯ N = 0,15 R a L 1 3

N u ¯ N = 0,15 ⋅ 9,60 × 10 7 1 3

N u ¯ N = 68,7

Como:

N u ¯ N = h ¯ L k = 68,7

Calculando o coeficiente de convecção:

h ¯ ⋅ 0,250 0,030 = 68,7

h ¯ = 8,24   W / m 2 ⋅ K

Calculando a taxa de transferência de calor:

q = h ¯ A s T s - T ∞

q = h ¯ L 2 T s - T ∞

Substituindo os dados:

q = 8,24 ⋅ 0,250 2 ⋅ 125 - 29

q = 49,44   W

Passo 4

Para a placa com movimento de ar, R e L = 5,98 × 10 3 e o fluxo é laminar:

N u ¯ F = 0,664 R e L 1 2 P r 1 3

N u ¯ F = 0,664 ⋅ 5,98 × 10 3 1 2 ⋅ 0,700 1 3

N u ¯ F = 45,6

Para convecção forçada livre combinada, usamos a relação com n = 7 / 2 :

N u ¯ 7 2 = N u ¯ N 7 2 + N u ¯ F 7 2

Então:

N u ¯ 7 2 = 68,7 7 2 + 45,6 7 2

N u ¯ = 73

Calculando o coeficiente de convecção:

h ¯ ⋅ 0,250 0,030 = 73

h ¯ = 8,76   W / m 2 ⋅ K

Calculando a taxa de transferência de calor:

q = 8,76 ⋅ 0,250 2 ⋅ 125 - 29

q = 52,56   W

Resposta

q = 49,44   W

q = 52,56   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um objeto com comprimento característico de 0,01 5m e uma situação na qual a diferença de temperaturas é de 1 0° C . Estimando as propriedades termofísicas nas condições especificadas, deter
Seja uma grande placa vertical com uma temperatura superficial uniforme de 100 ° C suspensa em ar quiescente a 25 ° C e a pressão atmosférica.(a) Estime a espessura da camada-limite em uma posição a 0
Um número de placas delgadas deve ser resfriado pela sua suspensão, em posição vertical, no interior de um banho de água a 20 ° C . Se as placas estão inicialmente a60 ° C e têm 0,10m de comprimento,
Um aquecedor elétrico com a forma de um disco horizontal com 500m m de diâmetro é usado para aquecer o fundo de um tanque de óleo de motor a uma temperatura de 10° C . Calcule a potência necessária pa
O escoamento de ar através de um longo duto de ar-condicionado, com formato quadrado e 0 , 3m de lado, mantém sua superfície externa a uma temperatura de 1 5° C . Se o duto, na posição horizontal, não