Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 61
61 – Considere a placa da base de um ferro de passar de , espessura , área da base e condutividade térmica . A superfície interna da placa está sujeita a um fluxo de calor uniforme gerado pela resistência do ferro. Quando alcança condições de operação permanente, a temperatura da superfície externa da placa mede . Desconsiderando qualquer perda de calor através da seção superior do ferro, (a) expresse a equação diferencial e as condições de contorno para condução de calor unidimensional permanente através da placa, (b) obtenha a relação para a variação da temperatura na placa da base do ferro resolvendo a equação diferencial e (c) avalie a temperatura da superfície interna.
Passo 1
Para começar com o pé direito, vamos desenhar um esqueminha!!!
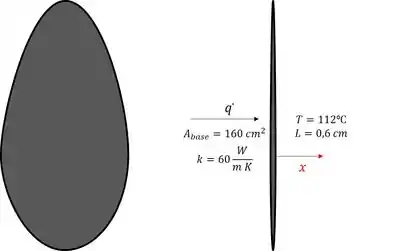
Temos então uma figura da base do ferro e do lado direito é a base do ferro de ladinho, como acontece a transferência de calor!
A letra (a) pede a equação diferencial e as condições de contorno para condução de calor unidimensional permanente através da placa. Então bora lá!
Passo 2
Para descrever esse caso a gente vai considerar regime permanente sem geração de calor, logo:
Então precisamos de 2 condições de contorno!!
Pela lei de Fourier:
Mas precisamos encontrar :
Aqui, é a capacidade desse ferro e é a área da base da chapa, substituindo por e para !
Calculando:
Achamos quando
Então podemos escrever nossa primeira condição de contorno!
Aqui, é a condutividade térmica da placa.
E a segunda condição de contorno está na temperatura da superfície externa da placa de base,
Em , a temperatura da superfície externa é
Passo 3
Agora vamos para letra b!!
(b) obtenha a relação para a variação da temperatura na placa da base do ferro resolvendo a equação diferencial
Para começar, temos:
Vamos precisar integrar essa equação 2 vezes, para isso já temos as condições de contorno encontradas na letra a!!
A derivada é igual a zero, isso quer dizer que ela é uma derivada de uma constante! Então quando integramos a primeira vez, temos:
Para
Substituindo:
Substituindo na equação original:
Integrando novamente:
Para ;
Calculando :
Substituindo na nossa expressão para a temperatura:
Passo 4
Pra acabar, temos que achar a temperatura na parte interna, ou seja, quando .
Para isso vamos substituir na equação que terminamos de achar!
Portanto, a temperatura da superfície interna é .
Observe que a temperatura da superfície interna é mais alta que a temperatura da superfície exposta quando são alcançadas condições de operação estáveis.
Resposta
a)
Primeira condição de contorno:
Segunda condição de contorno:
b)
c) .