Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 73

Considere um processo em batelada no qual 200   litros de um fármaco são aquecidos de 25 ° C a 70 ° C , por vapor de água saturado se condensando a 2,455   b a r quando escoa através de uma serpentina com tubo de 15   m m de diâmetro e 15   m de comprimento. Em qualquer instante durante o processo, o líquido pode ser aproximado por um meio quiescente infinito, com temperatura uniforme, e pode ser considerado com propriedades constantes iguais a: ρ   =   1100   k g / m 3 , c   =   2000   J / ( k g   ·   K ) , k   =   0,25   W / ( m   ·   K ) , v   =   4,0   ×   10 6     m 2 / s , P r   =   10 e β   =   0,002   K – 1 . As resistências térmicas no vapor condensando e na parede do tubo da serpentina podem ser desprezadas.

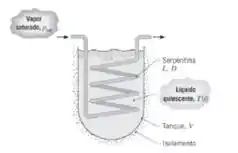
( a ) Qual é a taxa de transferência de calor inicial para o fármaco?

( b ) Desprezando a transferência de calor entre o tanque e sua vizinhança, quanto tempo demora para aquecer o fármaco até 70 ° C ? Represente graficamente a variação com o tempo correspondente da temperatura do fluido e do coeficiente convectivo na superfície externa da serpentina. Quanto vapor é condensado durante o processo de aquecimento?

Passo 1

Muito bem galera, entendendo a física por trás do que exercício pede...

Temos que a questão ( a ) , nos pede pra determinar qual a taxa de transferência de calor inicial que é transferida pro fármaco.

Do enunciando, podemos desconsiderar as resistências da parede, logo temos aqui um problema sob a influência de convecção natural, portanto a equação base é:

q = h - A s T s - T i

Passo 2

Além disso, o enunciado nos dá todos os dados que iremos precisar, ou seja:

ρ   =   1100   k g / m 3 , c   =   2000   J / ( k g   ·   K ) , k   =   0,25   W / ( m   ·   K ) , v   =   4,0   ×   10 - 6     m 2 / s , P r   =   10 e β   =   0,002   K – 1

Voltando para a física do problema, note que devemos determinar o coeficiente de convecção, ou seja, h - ...

Porém, precisamos antes, escolher uma correlação adequada para o problema. No caso podemos aproximar a serpentina para um cilindro horizontal.

Passo 3

Próximo passo é determinar o Rayleigh:

R a D = g β T s - T i D 3 υ α

α = υ P r = 4,0   ×   10 - 6   m 2 s 10 = 4,0   ×   10 - 7   m 2 s

Onde temos que, T s equivale a nossa temperatura na parede da serpentina, e o que equivale também a nossa temperatura de saturação, visto que vapor de água saturada escoa no interior e se condensa na parede.

Sendo assim, podemos utilizar a pressão de vapor saturado indicada pelo enunciado para determina-la pela tabela A-6 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.).

T s a t = 400   K = 127   ℃

Passo 4

Substituindo os valores...

R a D = 9,8 m s 2 0,002   K - 1 127 - 25 ℃ 0,015   m 3 4,0   ×   10 - 6     m 2 / s ( 4,0   ×   10 - 7   m 2 s ) = 4,22 × 10 6

Portanto, nossa correlação é:

N u - D = 0,60 + 0,387 R a D 1 6 1 + 0,559 P r 9 16 8 27 2

N u - D = 0,60 + 0,387 R 4,22 × 10 6 1 6 1 + 0,559 10 9 16 8 27 2 = 27,7

Passo 5

Agora podemos determinar nosso coeficiente de convectivo:

N u - D = h - k D

h - = 27,7 0,250 W m ∙ K 0,015   m = 462 W m 2 ∙ K  

E por fim...

q = h - A s T s - T i

Onde...

A s = π D L = π 0,15 ( 15 ) = 0,707   m 2

Portanto a taxa de calor inicial transferida para o fármaco é:

q = 462 W m 2 ∙ K 0,707   m 2 102 ° C = 33.300   W

q = 33.300   W

Resposta

A taxa de calor inicial transferida para o fármaco é:

q = 33.300   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A radiação solar incide sobre a cobertura de vidro de um coletor solar a uma taxa de 650 W/m2. O vidro transmite 88% da radiação incidente e tem emissividade de 0,9. As necessidades de água quente da
Os gases de escape de uma fábrica são expelidos por uma chaminé de exaustão de 10 m de altura com diâmetro externo de 1 m. Os gases de escape são descarregados a uma taxa de 0,125 kg/s, enquanto a que
Uma caixa de gelo cujas dimensões externas são 30 cm x 40 cm x 40 cm é feita de isopor ( k = 0,033 W/m.K) de 3 cm de espessura. Inicialmente, a caixa é preenchida com 35 kg de gelo a 0°C, e a temperat
Duas esferas concêntricas com raios de 5 cm e 10 cm estão tendo as temperaturas de superfície mantidas a 200°C e 100°C, respectivamente. O espaço entre as duas superfícies esféricas concêntricas é pre
Um tanque esférico de 4 m de diâmetro contém água com gelo a 0°C. O tanque é de casca fina, portanto a temperatura da superfície externa pode ser considerada igual à temperatura da água com gelo no in