Considere um recipiente exposto a um vapor saturado, , que tem uma superfície inferior fria, e com paredes laterais isoladas.

Admitindo uma distribuição de temperaturas linear no líquido, efetue um balanço de energia na interface líquido–vapor para obter a expressão a seguir para a taxa de crescimento da camada de líquido:
Calcule a espessura da camada de líquido formada em , para uma superfície inferior com , mantida a e exposta a vapor de água saturado a . Compare esse resultado com o condensado formado em uma placa vertical com as mesmas dimensões e no mesmo período de tempo.
Passo 1
Vamos lá! Nosso problema pede a espessura da camada para duas situações diferentes, mas antes não vamos esquecer do nosso velho esboço pra facilitar nosso problema.
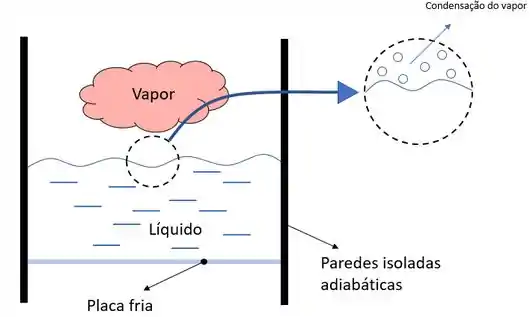
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá! Iremos usar os dados da tabela para água liquida saturada e água vapor saturado, temos que a taxa de condensação por unidade de comprimento é dada por:
Fazendo o balanço de energia temos:
Onde é o fluxo de calor pela condensação do vapor e é a condução do vapor na camada líquida de espessura , reorganizando a equação acima e integrando temos:
Assim chegamos:
Assim temos que a massa de vapor convertida em liquido nesse período é dada por:
Passo 3
Agora vamos comparar o resultado com a alternativa apresentada no problema para a placa vertical temos que o comprimento da placa é dado por , da equação :
Onde:
Como a equação nos diz que:
Assim finalmente temos que:
Como podemos observar tem grandeza quase vezes maior que , pois a taxa de condensação é constante enquanto na placa no fundo, pois com o passar do tempo a resistência condutiva aumenta com o aumento da camada.
Isso é tudo pessoal! \o/

Resposta
.
Aumenta quase vezes.