Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 129
Uma operação de transferência de massa é precedida pelo escoamento laminar de uma espécie gasosa B através de um tubo circular suficientemente longo para que se obtenha um perfil de velocidades plenamente desenvolvido. Uma vez atingida a condição plenamente desenvolvida, o gás entra em uma seção do tubo que se encontra molhada com um filme de um líquido (A). Este filme mantém uma concentração mássica do vapor uniforme ao longo de toda a superfície do tubo.
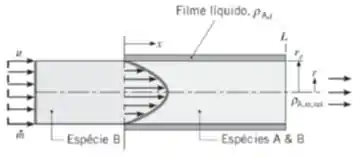
- Escreva a equação diferencial e as condições de contorno que governam a distribuição de concentrações mássicas da espécie A, , para .
- Qual é o problema análogo a esse na transferência de calor? Com base nesse análogo, escreva uma expressão para o número de Sherwood médio associado à troca de massa ao longo da região .
- Partindo da utilização do princípio da conservação de uma espécie em um volume de controle diferencial , deduza uma expressão (Equação 8.86) que possa ser usada para determinar a concentração mássica média do vapor, , em .
- Considere condições nas quais a espécie B é o ar, a 25 °C e 1 atm, e o filme líquido é formado por água, também a 25 °C. A vazão mássica é e o diâmetro do tubo é . Qual é a concentração média do vapor na saída do tubo, se ?
Passo 1
Eita! Muitas letras para resolvermos. Chega cansa uma questão dessa!
Precisamos começar devagar. Assim, vamos pela letra a).
Ela nos pede para determinarmos a equação diferencial para o nosso problema.
O interessante é que essa equação é bem semelhante a uma equação que já vimos antes. Ela é a seguinte equação diferencial para determinação da distribuição de temperatura:
E qual é a mudança que temos que fazer? São duas: o termo de difusividade, da térmica para mássica e a variável no termo diferencial, da temperatura para a concentração .
Sendo assim, temos a seguinte equação diferencial:
E as condições de contorno ao qual o nosso problema está submetido são:
E assim terminamos a letra a).
Passo 2
Agora, temos que encontrar uma expressão para o número de Sherwood médio. Para isto, precisamos entender qual é o problema análogo a esse na transferência de calor.
Como o contato com o filme líquido é após o desenvolvimento completo da camada hidrodinâmica, temos um problema de comprimento de entrada térmico.
Então, já sabemos qual é a relação para o número de Nusselt que devemos utilizar. Ela é:
Agora, basta mudarmos o número de Nusselt pelo número de Sherwood e o número de Prandtl pelo número de Schmidt.
Passo 3
Nosso trabalho agora é obter uma equação para determinar a concentração média de saída. Para este problema, auxilia muito um simples diagrama de um volume de controle, definindo quais os termos que “entram” no volume e quais que “saem”. Então,
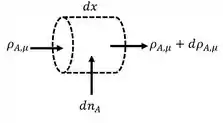
Bom, o que temos ai em cima é: na seção transversal, entra uma vazão mássica de , e sai uma vazão mássica de . Notem quem temos vazão constante, por isto não diferenciamos a relação velocidade x área transversal da entrada e da saída.
Só que nós não temos apenas este termo. Temos um termo “entrando” no volume de controle também. Este termo é devido a diferença entre o líquido ou sólido com densidade pelo gás que sai pela superfície lateral. Portanto, podemos descrever este termo da seguinte forma:
Agora que discutimos todos os termos que estarão no nosso balanço de massa, vamos fazê-lo então! Sendo assim, se a massa que entra é igual a massa que sai, temos:
Na equação que estamos buscando aparece o termo . Então, vamos fazer ele aparecer ai em cima. Para isto, basta lembrar que:
Então,
Se separarmos os termos diferenciais, temos:
Agora, só nos resta integrarmos a equação diferencial acima. Se integrarmos do ponto inicial e até o ponto final e , teremos:
Para tornarmos exatamente igual a Equação 8.86, basta aplicar a função exponencial em ambos os membros. Com isto, obtemos:
E assim, temos uma relação para calcular . Basta substituir na relação acima.
Passo 4
Agora, vamos finalizar a questão com chave de ouro! Vamos utilizar as relações que desenvolvemos anteriormente para obtermos a concentração média do vapor na saída do tubo.
Para conseguir isto, vamos precisar do coeficiente de convecção de massa . E para este, vamos precisar do número de Reynolds.
Bom, independentemente do que vamos calcular, vamos precisar de algumas propriedades do ar, da água e da mistura ar + vapor. Então, vamos aproveitar para determinar tudo de uma vez só.
Para o ar, que está a 1 atm e 298 K, temos, da Tabela A.4: , , .
Da água, vamos aproximar a sua densidade pela de vapor saturado a 298 K. Então, da tabela A.6, temos .
Para finalizarmos esta parte das tabelas, para a mistura de ar + vapor, temos: e .
Passo 5
Agora sim, podemos partir para os cálculos. Primeiro, começaremos pelo número de Reynolds, temos:
Agora, vamos calcular o coeficiente convectivo através da relação para o número de Sherwood que encontramos anteriormente. Sendo assim, temos:
Substituindo os valores das constantes:
Agora sim, podemos calcular a concentração na saída do tubo. Usando a relação que obtivemos no final do Passo 3, temos:
Resposta
- A equação diferencial é:
- Relação desenvolvida no Passo 3.
As condições de contorno são: