Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 126

Com referência ao Comentário 4 do Exemplo 5.12 , analise a súbita exposição da superfície a uma grande vizinhança, a uma temperatura elevada ( T v i z ) , e a condições de convecção ( T ∞ ,   h ) .

(a) Deduza a equação de diferenças finitas explícita para o nó na superfície em termos de F o ,   B i e B i r .

(b) Obtenha o critério de estabilidade para o nó na superfície. Esse critério muda com o tempo? Esse critério é mais restritivo do que o critério para um nó interior?

(c) Uma placa espessa de um material ( k   =   1,5   W / ( m   ·   K ) ,   a   =   7   ×   10 - 7   m 2 / s ,   ε   =   0,9 ) , inicialmente a uma temperatura uniforme de 27 ° C , é subitamente exposta a uma grande vizinhança a 1000   K . Desprezando a convecção e usando um incremento espacial de 10   m m , determine as temperaturas na superfície e a 30   m m da superfície após um intervalo de 1   m i n .

Passo 1

Vamos lá! Nosso problema pede uma atenção maior para entendermos o que acontece para assim deduzirmos as propriedades do problema, mas antes de fazer o esboço vamos apresentar o bendito comentário 4 para entender do que se trata.

C o m e n t á r i o   4 - Uma condição mais geral de aquecimento radiante seria aquela na qual a superfície é subitamente exposta a uma grande vizinhança com uma temperatura elevada T v i z (Problema 5.126 ). A taxa líquida na qual radiação é transferida para a superfície pode, então, ser calculada pela Equação 1.7 . Considerando também a transferência de calor por convecção para a superfície, a aplicação da conservação de energia no nó da superfície fornece uma equação de diferenças finitas explícita na forma

ε σ T v i z 4 - T 0 p 4 + h T ∞ - T 0 p + k ⋅ T 1 p - T 0 p Δ x = ρ ⋅ Δ x 2 ⋅ c ⋅ T 0 p + 1 - T 0 p Δ t

O uso dessa equação de diferenças finitas em uma solução numérica é complicado em função de sua n ã o   l i n e a r i d a d e . Entretanto, a equação pode ser l i n e a r i z a d a pela introdução do coeficiente de transferência de calor por radiação h r , definido pela Equação 1.9 . A equação de diferenças finitas fica, então.

h r T v i z - T 0 p + h T ∞ - T 0 p + k ⋅ T 1 p - T 0 p Δ x = ρ ⋅ Δ x 2 ⋅ c ⋅ T 0 p + 1 - T 0 p Δ t

A solução pode ser efetuada da forma usual, embora o efeito do número de B i o t   r a d i a n t e   ( B i r   ≡   h r   Δ x / k ) deva ser incluído no critério de estabilidade e o valor de h r deva ser atualizado a cada etapa do cálculo. Se o método implícito for usado, h r é calculado em p + 1 , tornando necessário um cálculo iterativo a cada novo incremento de tempo.

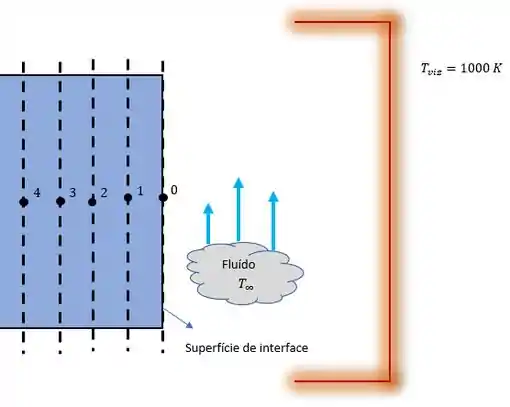
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - C o n d u ç ã o   t r a n s i e n t e   u n i d i m e n s i o n a l

I I - P r o p r i e d a d e s   c o n s t a n t e s

I I I - A   p l a c a   s e   c o m p o r t a   c o m o   u m   m e i o   s e m i - i n f i n i t o

I V - R a d i a ç ã o   e n t r e   u m a   s u p e r f í c i e   p e q u e n a   e   u m a   v i z i n h a n ç a   m u i t o   m a i o r

Passo 2

(a)

Vamos lá, com nossos dados em mãos vamos podemos chegar na equação do comentário 4 fazendo um balanço de energia pro nó de superfície, assim temos:

E ˙ e n t r a - E ˙ s a i = E ˙ a c u

h r T v i z - T 0 p + h T ∞ - T 0 p + k ⋅ T 1 p - T 0 p Δ x = ρ ⋅ Δ x 2 ⋅ c ⋅ T 0 p + 1 - T 0 p Δ t

Sendo nosso h r para o nó 0 :

h r T v i z ,   T 0 p = ε σ   T 0 p + T v i z ⋅ T 0 p 2 + T v i z 2

Dividindo a equação resultante do balanço de energia por: ρ ⋅ Δ x ⋅ c / 2 Δ t , temos:

T 0 p + 1 - T 0 p = k ⋅ 2 Δ t ⋅ T 1 p - T 0 p ρ ⋅ c ⋅ Δ x 2 + 2 Δ t ⋅ h T ∞ - T 0 p Δ x ⋅ ρ ⋅ c + 2 Δ t ⋅ h r T v i z - T 0 p Δ x ⋅ ρ ⋅ c

Organizando nossa equação para ela ter aparência de uma equação de métodos de elementos finitos temos:

T 0 p + 1 = 2 F 0 T 1 p + B i ⋅ T ∞ + B i r T s u r + 1 - 2 F 0 - 2 B i ⋅ F 0 - 2 B i r ⋅ F 0 T 0 p

Com:

F 0 ≡ k ρ ⋅ c ⋅ Δ t Δ x 2

B i ≡ h Δ x k

B i R ≡ h r Δ x k

Passo 3

(b)

Sabemos do critério de estabilidade, que o termo que multiplica T 0 p , não pode ser negativo então para a equação:

T 0 p + 1 = 2 F 0 T 1 p + B i ⋅ T ∞ + B i r T s u r + 1 - 2 F 0 - 2 B i ⋅ F 0 - 2 B i r ⋅ F 0 T 0 p

1 - 2 F 0 - 2 B i ⋅ F 0 - 2 B i r ⋅ F 0 ≥ 0

1 - 2 F 0 1 + B i + B i r ≥ 0

Reorganizando:

F 0 ≤ 1 2 1 + B i + B i r

Ou seja, F 0 ≤ 1 / 2 , pois B i + B i r > 0 , dessa forma temos que o critério de superfície é mais restritivo devido B i r variar com o tempo, devido h r aumentar com o tempo, assim a restrição para F 0 vai aumentar com o tempo.

Passo 4

(c)

Vamos lá, nossa letra (c) nos diz que podemos desprezar a convecção, assim temos:

Para o nó de superfície:

T 0 p + 1 = 2 F 0 T 1 p + B i r T s u r + 1 - 2 F 0 - 2 B i ⋅ F 0 - 2 B i r ⋅ F 0 T 0 p

Como podemos desprezar a convecção B i = 0 , assim:

T 0 p + 1 = 2 F 0 T 1 p + B i r T s u r + 1 - 2 F 0 - 2 B i r ⋅ F 0 T 0 p

O critério de estabilidade para essa situação fica assim:

F 0 ≤ 1 2 1 + B i r

Para os nós intermediários:

T m p + 1 = F 0 T m + 1 p + T m - 1 p + 1 - 2 F 0 T m p

Agora precisamos encontrar nosso intervalo de tempo, se fizermos Δ t = 15   s , vamos encontrar F 0 = 0,105 , para provar a escolha temos que na condição inicial:

h r 1000 ,   300 = 0,9 ⋅ 5,67 ⋅ 10 - 8 ⋅   300 + 1000 ⋅ 300 2 + 1000 2

h r = 72,3 W m 2 ⋅ K

502,289

Assim:

B i R = 72,3 W m 2 ⋅ K ⋅ 0,01   m 1,5 W m ⋅ K = 0,482

Do critério de estabilidade para essa equação temos que F 0 ≤ 0,337 , se fizermos as mesmas contas para T 0 = 800   K temos que: h r = 150 , 6 W m 2 ⋅ K , B i R = 1,004 e F 0 ≤ 249 .

Então não temos problema algum em utilizarmos nosso incremento de tempo como 15 segundos, agora montando uma tabela com nossos dados, temos:

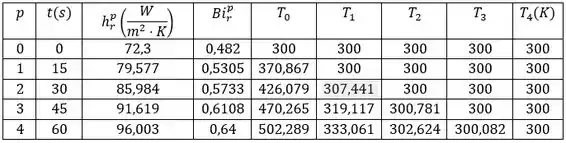
Então ao passar de 1 minuto, temos:

T s u r = T 0 60 = 502,289   K

T 30 m m = T 3 60 = 300,082   K

Isso é tudo pessoal! \o/

Resposta

(a) T 0 p + 1 = 2 F 0 T 1 p + B i ⋅ T ∞ + B i r T s u r + 1 - 2 F 0 - 2 B i ⋅ F 0 - 2 B i r ⋅ F 0 T 0 p

(b) F 0 ≤ 1 2 1 + B i + B i r . Sim varia com o tempo.

(c) T s u r = 502,289   K , T 30 m m = 300,082   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para escoamento incompressível laminar totalmente desenvolvido através de um duto retilíneo de seção não circular, como na seção 6.8, as equações de Navier-Stokes (4.38) se reduzem a ∂ 2 u ∂ y 2 + ∂ 2
Uma longa barra com seção transversal retangular, de 60m m × 90m m , tem condutividade térmica igual a 1W / m · K . Uma superfície está exposta a um processo de convecção com ar a 100°C e um coeficien
Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 4 00m m de lado. As paredes são construídas com tijolos refratários com 20 0m m de espessura e condutivid
Considere uma aleta plana triangular, bidimensional, com comprimento L = 50m m e espessura na base de t = 20m m . A condutividade térmica da aleta é k = 25W / m · K . A temperatura de sua base é T b =
47 – Canais quadrados de dimensão LC = 20,5(10 mm) = 14,14 mm são uniformemente espaçados em S=25 mm ao longo da linha central de um prato de espessura Lp= 40 mm. Fluido frio e quente escoam através d