Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 87

Uma canoa é representada por um semicilindro circular reto, com R = 0,35   m e L = 5,25   m . A canoa flutua sozinha em água com seu fundo a uma profundidade d = 0,245   m . Estabeleça uma expressão algébrica geral para a massa total (canoa e carga) que pode

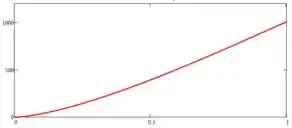
flutuar em função da profundidade. Avalie para as condições dadas. Plote os resultados para a faixa de profundidade na água 0 ≤ d ≤ R .

Passo 1

Nessa questão temos uma canoa, modelada como uma concha cilíndrica semicircular direita, flutua na água de profundidade d . Devemos encontrar uma expressão para a massa total máxima que pode ser flutuada, em função da profundidade, além de avaliar para as condições dadas e plotar para profundidade da água entre 0 e R .

Agora vamos ver com quais expressões podemos calcular isso:

d p d y = ρ g , pressão hidrostática onde y é positivo para a superfície livre.

F v = ∫ p d A y , força hidrostática vertical

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando na superfície da agua.

Passo 2

Inicialmente temos que y é uma função de θ para uma dada profundidade d e assim, temos o diagrama:

y = d - R - R cos ⁡ θ = d - R + R cos ⁡ θ

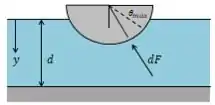
Assim, o máximo valor para θ é: θ m a x = acos ⁡ R - d R = acos ⁡ 0,35   m - 0,245   m 0,35   m = 1,27 . Pelo diagrama temos:

∑ F y = M g - F v

Passo 3

Pela força vertical,

F v = ∫ p d A y = ∫ p cos ⁡ θ d A

= ∫ - θ m a x θ m a x ρ g y L R c o s   θ d θ

= 2 ρ g L R ∫ 0 θ m a x ( d - R + R cos ⁡ θ ) c o s   θ d θ

Logo,

= 2 ρ g L R ∫ 0 θ m a x [ d - R cos ⁡ θ + R cos ⁡ θ 2 ] d θ

= 2 ρ g L R d - R sin ⁡ θ m a x + R θ m a x 2 + sin ⁡ 2   θ m a x 4

Como M = F v g , então:

M = 2 ρ L R d - R sin ⁡ θ m a x + R θ m a x 2 + sin ⁡ 2   θ m a x 4

Substituindo os dados:

M = 2 × 999 k g m 3 × 5,25 × 0,35 × 0,245   - 0,35   sin ⁡ ( 1,27 ) + R ( 1,27 ) 2 + sin ⁡ 2 × 1,27 4

M = 3671,325 - 0,105   sin ⁡ ( 1,27 ) + 0,35 × 0,272

Passo 4

Assim, o gráfico para os resultados para a faixa de profundidade na água 0 ≤ d ≤ R é:

Resposta

M = 18,72   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um densímetro flutua em um nível que é uma medida da densidade do líquido. A haste é de diâmetro constante D e o peso no fundo estabiliza o corpo para flutuar verticalmente, como mostra a Figura P2.10
Um balão de ar quente deve ser projetado para suportar o cesto, as cordas e uma pessoa, totalizando um peso de 1.300 N. O material do balão tem uma massa de 60 g/m2. O ar ambiente está a 25°C e 1 atm.
Uma boia de mastro é uma haste flutuante com peso ajustado para flutuar e sair verticalmente para fora, como mostra a Figura P2.113. Ela pode ser usada para medidas ou marcações. Considere que a boia
O balão da Figura P2.117 está cheio com hélio e pressurizado a 135 kPa e 20° C. O material do balão tem uma massa de 85 g/m2. Calcule (a) a tração na linha de ancoragem e (b) a altura que o balão vai
Um valente grupo de caçadores de tesouros descobriu uma caixa de aço, contendo dobrões de ouro e outros valores, sob uma profundidade de 24 m no mar. Eles calculam que o peso da caixa e do tesouro (no