Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 91

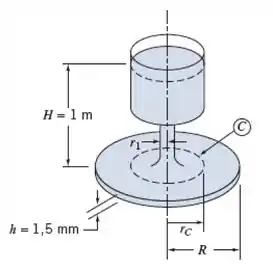
Considere o sistema de escoamento constituído de reservatório e discos, com o nível do reservatório constante, conforme mostrado. O escoamento entre os discos é iniciado do repouso em t = 0 . Avalie a taxa de variação da vazão volumétrica em t = 0 , se r 1 = 50   m m .

Passo 1

Vamos começar o exercício escrevendo a velocidade do fluido a partir da fórmula para a vazão do sistema, que pode ser dada por:

Q = V r A r = V r 2 π r h → V r = Q 2 π r h

Essa velocidade varia com r , e na extremidade temos r = R , logo:

V R = Q 2 π R h

Agora vamos aplicar a equação de Bernoulli para regime transiente entre o reservatório (ponto 1) e a saída do sistema (ponto 2), então, temos:

p 1 ρ + v 1 2 2 + g z 1 = p 2 ρ + v 2 2 2 + g z 2 + ∫ 1 2 ∂ V ∂ t d s

Nesse caso, como os pontos 1 e 2 estão expostos à atmosfera, temos p 1 = p 2 = p a t m = 0 , dessa forma, podemos cancelar os termos de pressão. Sabemos também que dentro do reservatório, podemos considerar v 1 = 0 , e vamos considerar o nível z 2 = 0 . Dessa forma, a equação se torna:

0 2 2 + g H = V R 2 2 + ∫ 1 2 ∂ V ∂ t d s

Passo 2

Agora vamos calcular o termo:

∫ 1 2 ∂ V ∂ t d s

Sabendo, do passo 1, que a equação para a velocidade em função de r é dada por:

V r = Q 2 π r h

Então, ela não depende do tempo, então podemos retirar a derivada parcial da integral, ficando com:

∂ ∂ t ∫ 1 2 V d s

Substituindo o valor de V r acima e sabendo que o nosso d s = d r , e que precisamos integrar de r 1 até R, temos:

∂ ∂ t ∫ r 1 R Q 2 π r h d r

Resolvendo a integral, temos:

∂ ∂ t Q l n ( r ) 2 π h r 1 R

Substituindo os limites de integração:

∂ ∂ t Q l n R 2 π h - Q l n r 1 2 π h

Pela propriedade dos logarítmos, podemos escrever:

∂ ∂ t Q l n R r 1 2 π h

Sabemos que o único termo que varia no tempo na expressão anterior é a vazão, então:

ln ⁡ R r 1 2 π h d Q d t

Passo 3

Agora vamos substituir a relação encontrada para a integral na equção de Bernoulli do passo 1:

g H = V R 2 2 + ∫ 1 2 ∂ V ∂ t d s → g H = Q 2 π r h 2 2 + ln ⁡ R r 1 2 π h d Q d t

O enunciado pediu para avaliar a taxa de vazão volumétrica para t = 0 , então, sabemos que para t = 0 → Q = 0 , substituindo esse valor na equação anterior, zeramos o segundo termo e ficamos com:

g H = ln ⁡ R r 1 2 π h d Q d t

Substituindo os valores conhecidos, temos (faltou o enunciado nos fornecer o valor de R , vamos usar o valor para que bata com o resultado do gabarito):

9,81 1 = ln ⁡ 0,3 0,05 2 π ( 0,0015 ) d Q d t → d Q d t = 5,16.10 - 2   m 3 / s 2

Resposta

d Q d t = 5,16.10 - 2   m 3 / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você (um jovem com idade permitida para beber) está fazendo cerveja caseira. Como parte do processo, você deve sugar o mosto (a cerveja fermentada com sedimentos no fundo) de um tanque limpo por meio
O seu carro fica sem combustível inesperadamente. Para você resolver o problema, você retira gasolina de outro usando um sifão. A diferença de altura do sifão é cerca de 150 mm. O diâmetro da mangueir
A contração de entrada e a seção de teste de um túnel de vento de laboratório estão esquematizadas na figura. A velocidade do ar na seção de teste é U = 50m / s . Um tubo pitot apontado diretamente pa
Um tubo pitot-estático é usado para medir a velocidade do ar na condição-padrão em um ponto de escoamento. A fim de assegurar que o escoamento possa ser considerado incompressível para cálculos de eng
Trabalhos de manutenção em sistemas hidráulicos de alta pressão exigem cuidados especiais. Um pequeno vazamento pode causar um jato de fluido hidráulico de alta velocidade que pode penetrar na pele e