Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 44
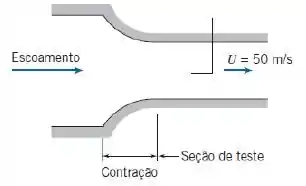
A contração de entrada e a seção de teste de um túnel de vento de laboratório estão esquematizadas na figura. A velocidade do ar na seção de teste é . Um tubo pitot apontado diretamente para montante no escoamento indica que a pressão de estagnação na linha de centro da seção de teste é 10 mm de água abaixo da pressão atmosférica. O laboratório é mantido na pressão atmosférica e à temperatura de -5°C. Avalie a pressão dinâmica na linha de centro da seção de teste do túnel de vento. Calcule a pressão estática no mesmo ponto. Qualitativamente, compare a pressão estática na parede do túnel com aquela na linha de centro. Explique por que as duas não podem ser idênticas.
Passo 1
Vamos começar o exercício calculando a densidade do ar para a condição dada através de:
Agora, sabemos que a pressão dinâmica no sistema é dada por:
Substituindo os valores conhecidos, temos:
E a pressão total é dada por:
Substituindo os valores conhecidos:
Passo 2
Agora podemos usar a equação para a pressão total para encontrar a pressão estática, então:
Substituindo os valores conhecidos:
Passo 3
A pressão estática na linha de centro e na parede não podem ser as mesmas porque existe um gradiente de pressão que varia na seção de uma seção curva, da forma:
Então, como esse gradiente de pressão depende da distância do centro, não podemos ter a mesma pressão na linha de centro e na parede da tubulação.