Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 33
Como observado no Problema 5.3, fornos de micro-ondas operam alinhando e revertendo moléculas de água no interior do alimento, resultando em geração volumétrica de energia e, desta maneira, no cozimento do alimento. Entretanto, quando o alimento está inicialmente congelado, as moléculas de água não oscilam facilmente em resposta às micro-ondas e as taxas de geração volumétrica ficam entre uma e duas ordens de grandeza menores em relação às taxas presentes se a água estivesse na forma líquida. (A potência das micro-ondas que não é absorvida no alimento é refletida de volta para o gerador de micro-ondas, onde deve ser dissipada na forma de calor para evitar danos ao gerador.)
(a) Considere um pedaço de carne congelada, esférico e com , a uma temperatura inicial de Ti = –20°C, no interior de um forno de microondas com e Determine quanto vai levar para a carne atingir uma temperatura uniforme de , com toda a água na forma de gelo. Suponha que as propriedades da carne são iguais às do gelo e considere que da potência do forno ( total) é absorvida no alimento.
(b) Após todo o gelo ser convertido em líquido, determine quanto tempo leva para aquecer a carne até se da potência do forno for absorvida no alimento. Suponha que as propriedades da carne são as mesmas da água líquida.
(c) Quando descongelamos alimentos em fornos de micro-ondas, é possível observar que parte do alimento permanece congelada enquanto outras partes são cozidas em demasia. Explique por que isto ocorre. Explique por que a maioria dos fornos de micro-ondas apresenta ciclos de descongelamento associados a potências muito baixas no forno.
Passo 1
Vamo lá galera! (a) Nós aplicamos a conservação de energia à carne:
A condição inicial é . Essa equação diferencial pode ser resolvida definindo:
Logo a equação se torna:
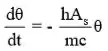
Separando variáveis e integrando,
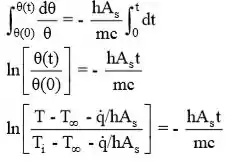
A taxa de geração de calor é dada por . O raio da esfera pode ser encontrado a partir do conhecimento da massa e da densidade:
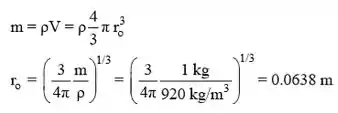
Logo,
Substituindo valores numéricos por Eq.(2), podemos encontrar o tempo em que a temperatura atinge 0°C:
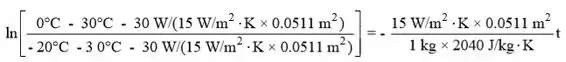
Portanto,
Passo 2
(b) Depois que todo o gelo é convertido em líquido, a potência absorvida é . O tempo para a carne chegar a pode ser novamente encontrado a partir de Eq.(2):
Portanto,
Passo 3
(c) A energia das microondas é absorvida de forma mais eficiente nas regiões de água líquida. Portanto, se o alimento ou a irradiação de microondas não for homogênea ou uniforme, a potência será absorvida de forma não uniforme, resultando em um aumento não uniforme da temperatura. As regiões descongeladas absorverão mais energia por unidade de volume do que as regiões congeladas. Se o alimento for de baixa condutividade térmica, não haverá tempo suficiente para a condução de calor para tornar a temperatura mais uniforme. O uso de baixa potência permite que mais tempo para a condução ocorra.