Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 34
Uma esfera de metal de diâmetro , que se encontra a uma temperatura uniforme , é subitamente removida de um forno e suspensa por meio de um fio fino em uma grande sala onde o ar está a uma temperatura uniforme e cujas paredes estão a uma temperatura .
(a) Desprezando a transferência de calor por radiação, obtenha uma expressão para o tempo necessário para resfriar a esfera até uma temperatura qualquer T.
(b) Desprezando a transferência de calor por convecção, obtenha uma expressão para o tempo necessário para resfriar a esfera até uma temperatura qualquer T.
(c) O que você faria para determinar o tempo necessário para resfriar a esfera até uma temperatura qualquer T se tanto a transferência por convecção quanto a transferência por radiação tivessem a mesma ordem de grandeza?
(d) Seja uma esfera de alumínio anodizado () com de diâmetro e que se encontra inicialmente a uma temperatura . Tanto o ar quanto a vizinhança se encontram a uma temperatura de , e o coeficiente convectivo é de Para as condições das partes (a), (b) e (c), determine o tempo necessário para a esfera resfriar até . Represente graficamente os históricos de temperatura correspondentes. Repita os cálculos para uma esfera de alumínio polido ().
Passo 1
Vamo lá galera! (a) Negligenciando a radiação, o tempo de resfriamento é previsto pela Eq. 5.5,
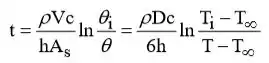
Passo 2
(b) Negligenciando a convecção, o tempo para arrefecer é previsto pela Eq. 5.18,
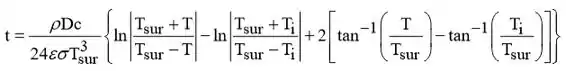
(c) Se a convecção e a troca de radiação forem consideradas, a necessidade de balanço energético resulta em Eq. 5.15. Portanto,
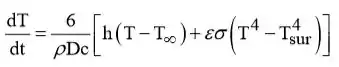
Passo 3
(d) Para a esfera de alumínio (puro) com acabamento anodizado e as condições prescritas, os tempos de resfriamento de a são:
1- Somente por convecção:
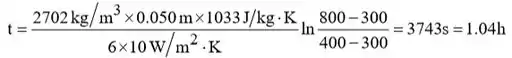
2- Somente por radiação:
Para radiação e convecção, usaremos a equação do passo 1. Temos um
Passo 4
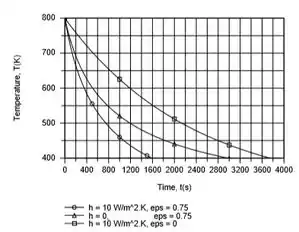
Neste caso, a perda de calor por radiação exerce uma maior influência, embora os efeitos da convecção não sejam de modo algum negligenciáveis. Contudo, se a superfície for polida (ε = 0.1), a convecção domina claramente. Para cada acabamento superficial e para os três casos, os históricos de temperatura são os seguintes.
