Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 17

Considere um tubo de ferro galvanizado, horizontal, de 5 cm de diâmetro. Qual deve ser a mínima queda de pressão da água, num trecho de 30 m de comprimento, para que o escoamento seja turbulento e hidraulicamente rugoso? Dados: γ á g u a = 10 4   N / m 3 ; μ á g u a = 10 - 3   N . s / m 2 .

Passo 1

Beleza, vamos começar calculando o ν da água (apesar de já termos usado várias vezes em outros exercícios e sabermos o valor):

ν = μ ρ = μ γ g = 10 - 3 10 4 10 → ν = 10 - 6   m 2 / s

Como vamos usar o diagrama de Moody nesse exercício, já vamos calcular o termo D H / k (lembrando de pegar o valor de k do quadro presente no próprio diagrama de Moody):

D H k = 0,05 1,52.10 - 4 → D H k = 330

Passo 2

Agora analisando o diagrama de Moody a seguir, vemos que o escoamento se torna hidraulicamente rugoso para a curva D H / k quando temos R e ≅ 4.10 5 .

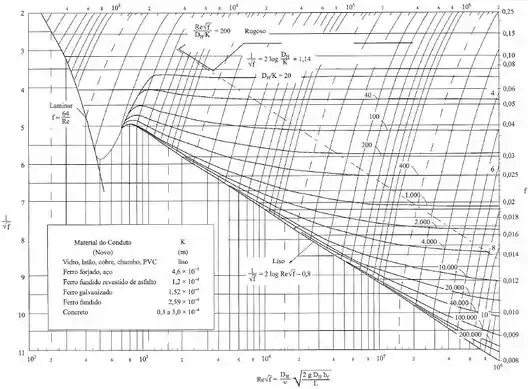
E, para essa condição de escoamento, temos:

f = 0,026

Dessa, forma, utilizando a fórmula de Reynolds para descobrir a velocidade do escoamento, temos:

R e = v D ν → v = ν R e D = 10 - 6 4.10 5 0,05 → v = 8   m / s

Passo 3

Agora podemos aplicar o equilíbrio de energia para o sistema entre o começo e o final do comprimento da tubulação, sendo assim, temos:

H 0 = H 1 + H p 0,1

v 0 2 2 g + p 0 γ + z 0 = v 1 2 2 g + p 1 γ + z 1 + H p 0,1

E, substituir os valores conhecidos (sabendo que podemos anular a velocidade e a diferença de altura, pois não temos mudança de geometria e nem de vazão no sistema e também não foi mencionada alteração de cota entre o começo e o fim da tubulação):

p 0 γ = p 1 γ + h f → p 0 - p 1 = Δ p = γ h f

E, a perda de carga distribuída é dada por:

h f = f L v 2 2 g D H

Substituindo os valores conhecidos:

h f = 0,026 30 8 2 2 10 0,05 → h f = 49,92   m

E, substituindo esse valor na equação para a diferença de pressão:

Δ p = 10 4 49,92 → Δ p = 499200   P a

Resposta

Δ p = 499200   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o menor duto retangular, liso e com razão de aspecto igual a 3, que deixará passar 1 m 3 s de ar a 10°C com uma perda de carga de 25 mm de água por 100 m de duto.
Petróleo está escoando de um grande tanque em uma colina para um petroleiro no cais. O compartimento de carga no navio está quase cheio e um operador inicia o processo de interrupção do escoamento. Um
Investigue o efeito do diâmetro de tubo sobre a vazão, calculando a vazão gerada por uma diferença de pressão, Δp = 100 kPa, aplicada a um comprimento L = 100 m de um tubo liso. Trace um gráfico da va
Água para resfriamento de perfuratrizes de rocha é bombeada de um reservatório para um canteiro de obras, usando o sistema de tubos mostrado. A vazão deve ser de 38 L s e a água deve deixar o bocal de
Um experimento de atrito de ar consiste de um tubo de latão liso de 63,5 mm de diâmetro interno; a distância entre tomadas de pressão é 1,52 m. A queda de pressão é indicada por um manômetro de tubo e