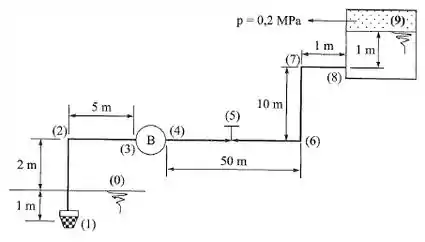
Na instalação da figura, determinar a potência da bomba necessária para produzir uma vazão de 10 L/s, supondo seu rendimento de 70%. Dados: ; ; aço; ; ; ; .
Passo 1
Nesse exercício, vamos calcular a perda de carga na parte antes e depois da bomba, para descobrir a perda de carga total e depois encontrar a carga e a potência da bomba, então, começando pelo trecho antes da bomba com :
Vamos então encontrar a velocidade nessa seção a partir da vazão e do diâmetro da tubulação:
Com isso podemos calcular o número de Reynolds dessa parte do escoamento:
Como vamos usar o diagrama de Moody nesse exercício, já vamos calcular o termo (lembrando de pegar o valor de para o aço do quadro presente no próprio diagrama de Moody):
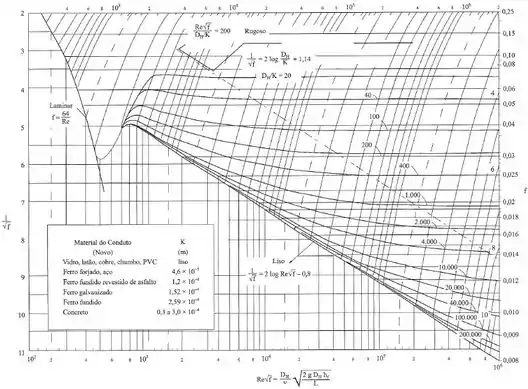
Então, para essa curva e para o valor de Reynolds encontrado, temos:
Passo 2
Dessa forma, substituindo os valores encontrados na equação para a perda de carga, temos:
Agora vamos escrever a perda de carga para o trecho após a bomba com :
Vamos então encontrar a velocidade nessa seção a partir da vazão e do diâmetro da tubulação:
Com isso podemos calcular o número de Reynolds dessa parte do escoamento:
Agora vamos calcular o termo :
Então, para essa curva e para o valor de Reynolds encontrado, temos:
Passo 3
Dessa forma, substituindo os valores encontrados na equação para a perda de carga, temos:
Além disso, o enunciado nos dá dois coeficientes de perda de carga localizada, que precisam ser considerados na perda de carga total:
Então, temos:
Dessa forma, a perda de carga total do sistema será:
Agora, aplicando o equilíbrio de energia entre os pontos 0 e 9, temos:
Substituindo os valores conhecidos:
Passo 4
Agora aplicando a equação da potência para uma bomba, temos: