Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 95
O corpo uniforme A da Figura P2.95 tem largura b e está em equilíbrio estático quando pivotado sobre a articulação O. Qual é a densidade desse corpo se (a) h = 0 e (b) h = R?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.6 do livro, chamada “Forças sobre superfícies curvas”.
Pra entender a questão, dá uma olhada na figura do enunciado. Temos um corpo pivotado sobre a articulação , do qual queremos encontrar a densidade para duas situações diferentes: quando ou .
Vamos dar uma olhada na representação das forças agindo na figura abaixo:
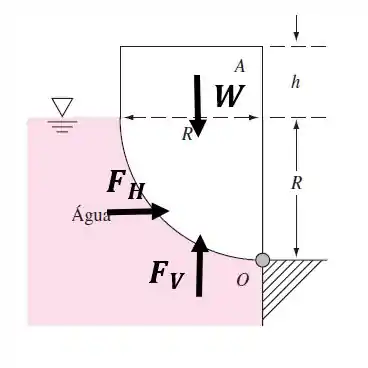
Sendo o peso do corpo de largura , a componente horizontal da força hidrostática e a componente vertical da força hidrostática.
Nos próximos passos, iremos descobrir como calcular essas forças e como usá-las para calcular a densidade do corpo.
Então, vamo lá matar esse problema juntos!
Passo 2
Primeiro, iremos calcular a componente horizontal Não iremos considerar a parte superior do corpo, pois a água está agindo apenas na geometria de quarto de círculo.
Para calcular essa componente, iremos considerar a projeção vertical dessa geometria, ou seja, devemos considerar a ação dessa força num retângula de base e altura .
Dessa forma, iremos utilizar a seguinte equação:
Sendo: o peso específico, que para água; a distância do centro de massa com relação à superfície livre, que para um retângulo é metade da altura do retângulo; e a área do retângulo projetado.
Dessa forma teremos:
Além disso, devemos calcular a linha de aplicação da componente horizontal da força em relação ao ponto , que podemos chamar de . Pra isso, vamos utilizar a equação abaixo:
Sendo: o ângulo entre a projeção e a horizontal, que, por definição, é 90°; e o momento de inércia para essa direção.
O momento de inércia de um retângulo, o próprio livro define na página 92 como :
Sendo: a largura do retângulo e a altura do retângulo, ou seja, . Logo:
Calculando então a linha de aplicação acima do ponto , temos:
Passo 3
Agora vamos calcular a componente vertical . Nesse caso, ela poderá ser calculada a partir do peso da água, com a equação:
Sendo o volume da água no corpo no formato de um quarto de círculo. Sendo assim, temos:
Pra calcular a linha de aplicação `a esquerda de para a componente vertical, basta ir novamente na página 92 e usar a mesma distância do centroide para um semi-círculo. Ou seja, a linha de aplicação pode ser calculada como:
Passo 4
Para calcular o peso do corpo, devemos dividir o corpo em duas geometrias: um paralelepípedo de lados na parte superior e um quarto de círculo de raio e largura . Sendo assim, o peso pode ser calculado como.
Chamaremos esses duas contribuições de peso, respectivamente, como e :
Sendo a densidade do sólido.
Agora, devemos estabelecer as linhas de aplicação dessas forças com relação ao ponto . Para o retângulo, basicamente essa linha estará a à esquerda de . Para o peso no quarto de círculo, ela estará a .
Passo 5
Por fim, precisamos calcular a densidade do corpo para as duas situações estabelecidas no enunciado. Para isso, devemos fazer um balanço de momento em torno de , em sentido horário, com as forças que calculamos nos Passos anteriores.
Sabemos que, para o corpo estar fixo, esse balanço deve ser zero:
Para o balanço de momento se torna:
Já para o balanço se torna:
Resposta
(a) A densidade desse corpo se é
(b) a densidade desse corpo se é