Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 105

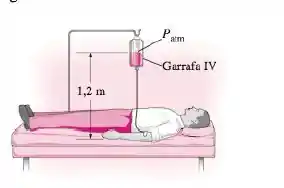
Infusões intravenosas em geral são movidas pela gravidade, pendurando-se a garrafa de fluido a uma altura suficiente para contrabalancear a pressão do sangue na veia e forçar o fluido a entrar no corpo. Quanto mais alto a garrafa for elevada, maior será a taxa de escoamento do fluido. (a) Se for observado que as pressões do fluido e do sangue se equilibraram quando a garrafa está a 1,2 m acima do nível do braço, determine a pressão manométrica do sangue. (b) Se a pressão manométrica do fluido no nível do braço precisar ser 20 k P a para que a taxa de escoamento seja suficiente, determine a altura da garrafa. A densidade do fluido é 1.020 k g m 3 .

Passo 1

Fala aí galerinha do responde aí, bora pra mais uma questão de Mecânica dos Fluidos. Na letra a temos que a pressão sanguínea será igual a pressão gerada pelo fluido (considerando a pressão atmosférica). Considerando a pressão atmosférica como 101 k P a , temos que:

P s a n g u e = 1,2 × g × 1.020 + 101000 = 12240 + 101000 = 113,24 k P a

Considerando g = 10 m s 2 .

Passo 2

Já para a letra b, o processo é inverso. Temos que P s a n g u e = 20 k P a .   Logo:

20 = h × g × 1.020

Logo:

h = 20000 10 × 1.020 = 1,96 m

Resposta

  1. P s a n g u e = 113,24 k P a
  2. h = 1,96 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta A B da figura tem 1,5m de largura e pode girar em torno de A . O tanque à esquerda contém água ( γ = 10.000N / m 3 ) e o da direita, óleo ( γ = 7.500N / m 3 ) . Qual é a força necessária em
Sabendo que γ 1 = 6 γ 2 , calcular a relação x / h para que a comporta permaneça em equilíbrio na posição indicada na figura. Desprezar o peso próprio da comporta.
No esquema da figura, determinar a altura h e a mínima força F para que a comporta A B C permaneça em equilíbrio. Dados: largura = 1,5m ; γ H g = 136000N / m 3 ; γ H 2 O = 10000N / m 3 .
A comporta da figura é rígida e pode girar em torno de B . Sabendo que está em equilíbrio, determinar o comprimento B C .
Determinar o mínimo valor de z para o qual a comporta da figura girará em torno de ponto O , se a comporta é retangular e tem largura 2m .