Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 45
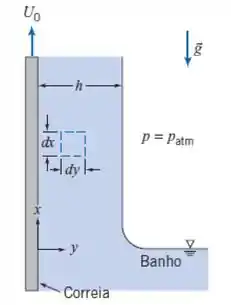
Uma correia contínua, movendo com velocidade para cima através de um banho químico, arrasta uma película de líquido de espessura , massa específica e viscosidade . A gravidade tende a fazer com que o líquido desça, mas o movimento da correia impede que ele retorne completamente. Admita que o escoamento seja laminar, completamente desenvolvido, com gradiente de pressão zero e que a atmosfera não produz tensão de cisalhamento na superfície externa da película. Enuncie claramente as condições de contorno a serem satisfeitas pela velocidade em e . Obtenha uma expressão para o perfil de velocidade.
Passo 1
Tá legal, vamos começar esse exercício aplicando o equilíbrio de momento na direção para o elemento diferencial ilustrado na figura do enunciado, então, temos:
Nesse caso, como temos regime permanente a derivada no tempo da integral sobre o volume de controle será igual a zero. Também temos escoamento totalmente desenvolvido, então a integral sobre a superfície de controle será igual a zero. Nesse caso, a equação irá se resumir às forças de superfície e a força de campo, então, teremos:
Em que é a força do lado oposto a correia e a força no elemento do lado da correia. Agora, conforme vimos no Exemplo 8.3, podemos escrever as tensões de cisalhamento nas faces esquerda e direita como:
Então, substituindo essas expressões na equação acima, temos:
Então, aplicando a distributiva e simplificando os diferenciais que aparecem em todos os termos, temos:
Passo 2
Agora vamos integrar a expressão obtida no passo 1 com relação a , então, teremos:
No entanto, sabemos que a tensão de cisalhamento pode ser escrita como:
Então, substituindo essa expressão na equação de cima, temos:
Agora, vamos integrar novamente essa expressão em , e chegaremos em:
Passo 3
Agora, para encontrar as constantes e para , vamos utilizar as condições de contorno que nós conhecemos, da ilustração do enunciado, temos que:
Então, substituindo esses valores na equação para , temos:
Agora, a outra condição de contorno é que na superfície em contato com o ambiente, não temos cisalhamento, dessa forma, temos:
Então, substituindo esses valores na equação abaixo, temos:
Então, a equação para o perfil de velocidade será: