Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 77

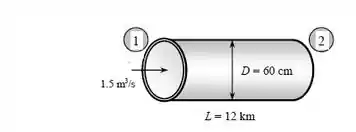
Um sistema de aquecimento distrital geotérmico envolve o transporte da água geotérmica a 110°C de um poço geotérmico para uma cidade com a mesma altitude por uma distância de 12 km, a uma vazão de 1,5 m³/s, em tubos de aço inoxidável com 60 cm de diâmetro. As pressões do fluido na superfície do poço e no ponto de chegada da cidade devem ser iguais. As perdas menores são desprezíveis devido à grande razão maior entre comprimento e diâmetro e ao numero relativamente pequeno de componentes que causam perdas menores. (a) Assumindo que a eficienda da bomba-motor seja de 74%, determine o consumo de energia elétrica do sistema para o bombeamento. Você recomendaria o uso de uma única bomba grande ou de diversas bombas menores com mesma potência total de bombeamento espalhadas pela tubuluação? Explique. (b) Determine o custo diário de cosumo de energia do sistema se o custo unitário da eletricidade for de $ 0,06/kWh. (c) A queda da temperatura da água geotérmicaé estimada como 0,5 °C durante esse escoamento longo. Determine se o aquecimento por atrito durante o escoamento pode compensar essa queda de temperatura.

Passo 1

Vamos pegar as propriedades da água a 110°C!!

ρ = 950   k g / m ³

μ = 0,255   x   10 - 3 k g m . s

C p = 4,229 k J k g . ° C

A rugosidade do tubo é de 2 x 10-6 m

Passo 2

  1. Vamos aplicar Bernoulli na nossa tubulação, se liga!

    2. P 1 ρ g + V 1 2 2 g + z 1 + h b o m b a = P 2 ρ g + V 2 2 2 g + z 2 + h L

    h b o m b a = h L

    Bem, sabendo a vazão, a gente consegue calcular a velocidade!!!

    V = Q A c = Q π D 2 4 = 1,5 π 0,6 2 4 = 5,3   m / s

    Próximo passo, bora calcular nossa rugosidade relativa do tubo ε D = 2   x   10 - 6 0,6 = 3,33   x   10 - 6

    Em seguida, o que precisamos calcular é tcharammm!!! O nosso fator de atrito e pra isso vamos usar a fórmula de Colebrook através de um processo iterativo ouuuuu, você pode com o valor de Reynold e o valor da rugosidade relativa, ir no diagrama de Moody.

    Lembrando que R e = ρ V D μ = 1,187   x   10 7

    1 f = - 2 log ⁡ ε D 3,7 + 2,51 R e f → f = 0,00829

    Calculando agora nossa perda de pressão como ∆ P = ∆ P L = f L D ρ V 2 2 = 2218   k P a

    h L = ∆ P L ρ g = 238   m

    Vamos calcular essa potência agora:

    W e l e t = W b o m b a e f i c i ê n c i a = Q ∆ P e f i c i e n c i a = 1,5 2218 0.74 = 4496   k W

    Então, a gente acabou de calcular que a bomba vai consumir isso aí de energia pra poder contornar o atrito e manter o escoamento. As bombas devem aumentar a pressão da água geotérmica em 2218 kPa. Fornecer um aumento de pressão dessa magnitude em um local apenas, pode criar tensão excessiva na tubulação naquele local. Portanto, é mais desejável aumentar a pressão em quantidades menores em vários locais ao longo do fluxo.

    Passo 3

  2. Quantidade de eletricidade usada por dia vai ser:

    3. W e l e t   x   ∆ t = 4496   x   24 = 107900 k W h d i a

    c u s t o = 107900   x   0,06 = $ 6474 / d i a

    Passo 4

  3. Bem, a gente sabe que o atrito gera calor, né?

A gente pode assumir então que W m e c â n i c o = ρ Q C p ∆ T → ∆ T = e f i c i e n c i a   x   W e l e t ρ Q C p = 0,55 ° C

Com isso, a gente vê que o atrito gerará 1,1°C no aumento da temperatura, o que é maior do que a queda 0,5°C possível, podendo manter a água na temperatura apropriada.

Resposta

  1. Welet = 4496 kW
  2. Custo = 6474 $/dia
  3. ∆ T = 0,55 °C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois fluidos imiscíveis estão contidos entre placas paralelas infinitas. As placas estão separadas pela distância 2 h , e as duas camadas de fluidos têm espessuras iguais, h ; a viscosidade dinâmica d
Dois fluidos imiscíveis estão contidos entre placas paralelas infinitas. As placas estão separadas pela distância 2h, e as duas camadas de fluidos têm a mesma espessura h = 5m m . A viscosidade dinâmi
A cabeça de leitura/gravação do disco rígido de um computador flutua acima do disco giratório sobre uma delgada camada de ar (a espessura do filme de ar é 0,25 μ m ). A cabeça está a 25 mm da linha de
A distribuição de velocidade em uma fina película de fluido escoando para baixo sobre uma superfície inclinada foi desenvolvida no Exemplo 5.9. Considere um filme de 7 mm de espessura de um líquido co
Dois líquidos imiscíveis de mesma massa específica estão escoando para baixo sobre uma superfície inclinada de 60° em relação à horizontal. As duas camadas de fluidos têm a mesma espessura h = 10m m ;