Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 79
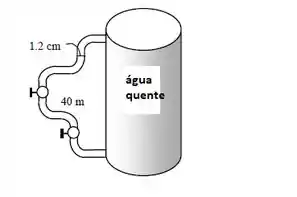
Em prédios grandes, a água quente de um tanque de água circula através de um laço, para que o usuário não tenha que esperar até que toda a água da tubulação longa drene antes que a água quente comece a sair. Determinado laço de recirculação envolve tubos de ferro fundido com 40 m de comprimento e 1,2 cm de diâmetro, com seis curvas suaves rosqueadas de 90° e dois distribuidores totalmente abertos. Se a velocidade média do escoamento através do laço é de 2,5 m/s, determine a entrada necessária de potência para a bomba de recirculação. Tome a temperatura média da água como 60°C e a eficiência da bomba como 80%.
Passo 1
Vamos tomar as propriedades da água em 60°C:
E consideraremos a rugosidade do tubo como 0,00026 m e que o coeficiente de perda KL = 0,9 para as rosqueaduras suaves de 90° e pras válvulas vamos considerar KL = 0,2.
Passo 2
Como sempre, quando desejamos saber eficiência de bomba, precisaremos usar nossa famosa equação de Bernoulli
Mas vamos prestar atenção no termo da perda de carga, porque sabemos que a bomba deve ter uma potência igual ou maior do que a perda de carga total que o sistema propõe ao escoamento, certo?
Onde
Vamos também calcular nossa rugosidade relativa
Fizemos isso tudo para podermos calcular nosso fator de atrito pela equação de Colebrook!!
Passo 3
Substituindo o valor do fator de atrito para calcular a perda de carga total:
E também calcula-se
Note que conhecendo a velocidade, calculamos a vazão Q da seguinte maneira:
Resposta
Wele = 0,217 kW