Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 29

Uma corrente de água uniforme U ∞ =   20   m / s e ρ =   998   k g / m ³ é combinada com uma fonte na origem para formar um semicorpo. Em (x, y) = (0, 1,2 m), a pressão é 12,5 kPa abaixo de p ∞ . (a) Esse ponto está fora do corpo? Calcule (b) a intensidade adequada da fonte m e (c) a pressão no nariz do corpo.

Passo 1

Bora pra mais uma!

Nós sabemos, da figura 8.5 e da equação 8.18, que o ponto na metade do corpo na superfície logo acima de “m” está em y = π a 2 , conforme mostrado na imagem abaixo, onde a = m U . A equação de Bernoulli nos permite calcular a força de fonte “m”, necessária da pressão em (x,y)=(0,1,2m).

P ∞ + ρ 2 U ∞ 2 = P ∞ + 998 2 20 2 = P ∞ - 12500 + 998 2 20 2 + m 1,2 2

(b) → m = 6,0 m ² / s

Sendo a = m U = 6 20 = 0,3 m

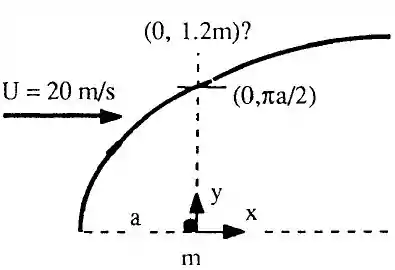
A superfície do corpo está em y = π a 2 = 0,47 m acima de “m”. (a) Portanto o ponto y=1,2m acima de m está fora do corpo.

No nariz do corpo, (x,y)=(-a,0), a velocidade é zero, portanto podemos prever:

P ∞ + ρ 2 U ∞ 2 = P ∞ + 998 2 20 2 = P n a r i z + ρ 2 0 2 ,  

→ P n a r i z = P ∞ + 200 k P a  

Resposta

(a) Portanto o ponto y=1,2m acima de m está fora do corpo.

P n a r i z = P ∞ + 200 k P a

(b) → m = 6,0 m ² / s

(c) P n a r i z = P ∞ + 200 k P a   .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Neste capítulo nós deduzimos a equação de continuidade de duas maneiras: usando o teorema da divergência e somando as vazões em massa através de cada face de um volume de controle infinitesimal. Expli
Se um campo de escoamento é compressível, o que podemos dizer sobre a derivada material da densidade? E se o campo de escoamento for incompressível?
Verifique se o campo de velocidade bidimensional, incompressível, permanente do Problema 9-16 satisfaz a equação de continuidade. Fique nas coordenadas cartesianas e mostre todo o seu trabalho.
No Exemplo 9–6, derivamos a equação para taxa de deformação volumétrica 1 V d V d t =∇ →.V → . Escreva isso como uma equação em palavra e discuta o que acontece com o volume de um elemento fluido à me
Repita o Exemplo 9–1 (gás comprimido em um cilindro por um pistão), mas sem usar a equação de continuidade. Em vez disso, considere a definição fundamental de densidade como massa dividida por volume.