Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 37

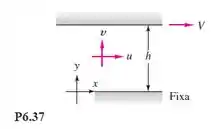
Duas placas infinitas separadas por uma distância h são paralelas ao plano xz, com a placa superior movendo-se com velocidade V, como na Figura P6.37. Existe um fluido de viscosidade μ a pressão constante entre as placas. Desprezando a gravidade e considerando escoamento turbulento e incompressível u ( y ) entre as placas, aplique a lei logarítmica e as condições de contorno apropriadas para deduzir uma fórmula para a tensão de cisalhamento adimensional na parede em função da velocidade adimensional da placa. Esboce uma forma típica do perfil u y .

Passo 1

Falaaaaaaaa, caraaaa! E estamos aqui juntos novamente, bora passar por cima de mais uma questão!

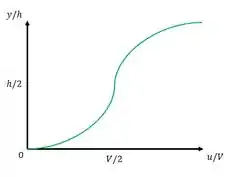
Cara, a tensão de cisalhamento entre as placas paralelas é constante, aí, vamos ter que a velocidade no ponto central é u = V / 2 em y = h / 2 , teremos um aumento na velocidade de 0 < y < h / 2 e um decréscimo em h / 2 < y < h , isso, se pegarmos de “trás pra frente”. Aí teremos um perfil mais ou menos assim ó:

Passo 2

Bora achar essa tensão de cisalhamento, teremos pela expressão logarítmica e as leis de contorno que:

V 2 u * ≈ 1 k ln ⁡ h u * 2 ν + B

Sendo, ν = μ / ρ , teremos:

V 2 u * ≈ 1 k ln ⁡ h u * ρ 2 μ + B

Tendo, k = 0,41   e   B = 5 , e pegando o ponto central, teremos que:

u * = τ w ρ 1 / 2  

Levando em consideração um valor de Reynolds entre 2000 < R e < 1 E 5 , conseguimos chegar num coeficiente de atrito adimensional que envolve a tensão de cisalhamento e o número de Reynolds, teremos que:

C f = τ w 1 2 ρ V 2 ≈ 0,018 ρ V h ν   1 4 = 0,018 R e 1 / 4

Resposta

C f = τ w 1 2 ρ V 2 ≈ 0,018 ρ V h ν   1 4 = 0,018 R e 1 / 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Glicerina a 40 ° C com ρ = 1,252k g / m 3 e μ = 0,27k g / m . s escoa através de um tubo suave horizontal com 5c m de diâmetro e velocidade média de 3,5m / s . Determine a queda de pressão por 10m do
Considere o escoamento laminar de um fluido através de um canal quadrado com superfícies suaves. Agora a velocidade média do flúido é dobrada. Determine a variação da perda de carga do fluido. Conside
Repita o Problema 8 - 33 para um tubo de raio interno de 7c m .
O ar entra em uma seção de 7m de comprimento de um duto retangular de seção transversal de 15c m× 20c m , feita de aço comercial, a 1a t m e 35 ° C , à velocidade média de 7m / s . Desprezando os efei
O perfil da velocidade no escoamento laminar completamente desenvolvido em um tubo circular de raio interno R = 2c m em m / s é dado por u r = 4 ( 1 - r 2 / R ² ) ² . Determine as velocidades média e