Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 14
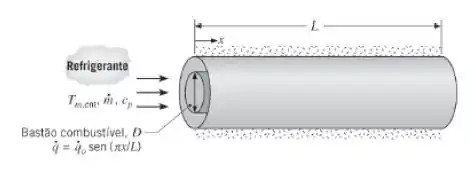
Seja um bastão cilíndrico de combustível nuclear, com comprimento L e diâmetro D, que se encontra no interior de um tubo concêntrico. Água pressurizada escoa na região anular entre o bastão e o tubo a uma vazão , e a superfície externa do tubo encontra-se isolada termicamente. Geração térmica ocorre no interior do bastão combustível e sabe-se que a taxa
volumétrica de geração varia senoidalmente com a distância ao longo do bastão. Isto é, , com sendo uma constante. Pode-se admitir um coeficiente de transferência de calor h uniforme entre a superfície do bastão e a água.
- Obtenha expressões para o fluxo térmico local e para a transferência de calor total q do bastão combustível para a água.
- Obtenha uma expressão para a variação da temperatura média da água com a distância x ao longo do tubo.
- Obtenha uma expressão para a variação da temperatura superficial no bastão com a distância x ao longo do tubo. Desenvolva uma expressão para determinar a posição x na qual essa temperatura é máxima.
Passo 1
Faaaaaaaaaaaaalaa galerinha!!
Bora continuar?!
Olhando mais de perto o que está acontecendo:
Para começar vamos fazer um balanço energético para o bastão combustível, percebam que ele gera energia térmica e transmite calor para a água:
Lembrando que:
Derivando:
Sabemos também que a energia gerada é dada por:
Como estamos analisando para um determinado volume de controle:
Portanto:
Achamos uma das respostas, certo?
Mas também queremos achar a transferência de calor total q do bastão combustível para a água.
Acabamos de ver que:
Substituindo
Integrando:
E chegamos ao fim da letra (a), mas já vamos seguir pra (b) !!
Passo 2
Na letra (b) queremos achar uma expressão para a variação da temperatura média da água com a distância x ao longo do tubo.
Aqui nós faremos um novo balanço, para a água:
Já sabemos , né?
Isolando a temperatura:
E integrando:
E é isso ai !! Boora pra (c)?
Passo 3
Na (c) e última letra nós precisamos de uma expressão para a variação da temperatura superficial no bastão com a distância x ao longo do tubo.
A lei do resfriamento nos diz que:
Isolando
Substituindo e
E como achamos a temperatura máxima?
O cálculo já diz, não é?
A temperatura máxima acontecerá quando
E isolando o que nós queremos:
Puxado, mas nada complicado, não é?
Resposta
- .