Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 5

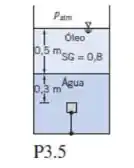
Um cubo de carvalho maciço, de volume 125 mL, é mantido submerso por um tirante, conforme mostrado. Calcule a força real da água sobre a superfície inferior do cubo e a tração no tirante.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede para encontrarmos a força real da água sobre a superfície inferior do tudo e a tração no tirante. Para resolvermos, temos que a pressão no inferior do cubo é dada por:

p I = P a t m + ρ g ( S G ó l e o ∙ h ó l e o + h I )

Pelos dados do cubo, temos:

V = 125 × 10 - 4   m 3

d 3 = V

Logo:

d = 0,05 m

E a altura na superfície do cubo é por:

h U = 0,3   m

Consequentemente:

h I = h U + d h I = 0,35   m

Agora, para calcularmos a força na parte inferior do cubo, temos:

                                                                                  F I = p I ∙ A

F I = p I ∙ d 2 F I = P a t m + ρ g S G ó l e o ∙ h ó l e o + h I ∙ 0,0025   m 2  

Substituindo:

F I = 270,89   N

Passo 2

Agora, para a força na parte superior, temos:

F S = P a t m + ρ g S G ó l e o ∙ h ó l e o + h U A

Podemos reescrever esta equação da seguinte forma:

∆ F = F I - F S = ρ g h I - h U A

Substituindo:

F U = 269,67   N

Por fim, temos:

S G = 0,77 W = S G ρ g V W = 0,944   N

Substituindo:

T = F I - F S - W T = 0,282   N

Resposta

F I = 270,89   N

F U = 269,67   N

T = 0,282   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema a seguir está aberto a 1 atm no lado direito. (a) Se L = 120 cm, qual é a pressão do ar no recipiente A? (b) Inversamente, se pA = 135 kPa, qual é o comprimento L?
A água escoa para baixo em um tubo a 45°, como mostrado a seguir. A queda de pressão p1 - p2 deve-se em parte à gravidade e em parte ao atrito. O manômetro de mercúrio indica uma diferença de altura d
Na Figura FE2.3, se o óleo da região B tem d = 0,8 e a pressão absoluta no ponto A é 1a t m , qual é a pressão absoluta no ponto B ? 5,6k P a 10,9k P a 107k P a 112k P a 157k P a
Um manômetro ligado a um tanque de nitrogênio pressurizado registra uma pressão manométrica de 711m m de mercúrio. Se a pressão atmosférica for de 101,3k P a , qual é a pressão absoluta no tanque? 95k
Em um dia normal ao nível do mar, um manômetro, colocado abaixo da superfície do oceano ( d = 1,025 ) , registra uma pressão absoluta de 1,4M P a . A que profundidade se encontra o instrumento? 4m 129