Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 21

É dada a função de corrente Ψ = x 2 + 2 x y + 4 t 2 y . No instante t = 2   s , determinar

  1. Qual é a vazão por unidade de espessura entre (A) e (B)
  2. Qual é a vazão por unidade de espessura entre (A) e (C)

Passo 1

A função de corrente para o ponto t = 2   é

Ψ = x 2 + 2 x y + 16 y

Podemos usar a equação 11.32 para encontrar as componentes da velocidade:

v x = ∂ Ψ ∂ y = ∂ x 2 + 2 x y + 16 y ∂ y ⇒ v x = 2 y + 16

v y = - ∂ Ψ ∂ x = - ∂ x 2 + 2 x y + 16 y ∂ x ⇒ v y = - 2 x - 2 y

Passo 2

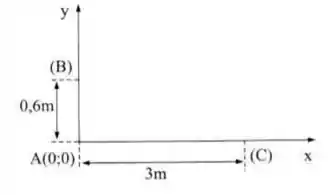
O gráfico da questão nos dá a distância entre os pontos. Então, basta integrar entre eles.

O fluxo que atravessa AB é composto pela velocidade v x , e a área por onde passa é igual a altura y e a uma espessura constante que chamaremos b . Os limites vão variar entre a altura inicial zero em (A) até a altura de B

Q A B = ∫ A B v x ⋅ d A

Q A B = ∫ 0 0,6 2 y + 16 ⋅ b ⋅ d y  

Q A B = b ⋅ y 2 - 16 y ​ 0 0,6  

Q A B = 9,6 ⋅ b m 3 s  

Dividindo os dois lados pela espessura:

q A B = 9,6 m 3 s ⋅ m

Passo 3

Fazemos o mesmo para AC

Q A C = ∫ A C v y ⋅ d A

Q A C = ∫ 0 3 - 2 x - 2 y ⋅ b ⋅ d x  

Perceba que pra qualquer ponto entre A e C o valor da altura é sempre zero! Ou seja ,   y = 0 ao longo de toda a integral.

Q A C = - 2 ∫ 0 3 x ⋅ b ⋅ d x  

Q A C = - x 2 ​ 0 3 ⋅ b  

Q A C = - 9 ⋅ b  

Dividindo os dois lados pela espessura: q A C = - 9 m 3 s ⋅ m  

Resposta

q A B = 9,6 m 3 s ⋅ m

q A C = - 9 m 3 s ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 9-51, criando a sua própria função corrente. Você pode criar qualquer função ψ ( x ,y ) que desejar, desde que ela contenha pelo menos três termos e não seja a mesma de um exemplo ou
Um campo de escoamento permanente, bidimensional, incompressível no plano x y tem a seguinte função corrente: ψ = a x 2 + b x y + c y 2 , onde a , b , e c são constantes. (a) Obtenha expressões para a
Um cálculo de CFD de escoamento permanente, incompressível, bidimensional através de uma ramificação de duto assimétrica bidimensional revela o padrão de linhas de corrente desenhado na Figura P9-53,
Um campo de escoamento permanente, bidimensional, incompressível no plano x y tem uma função corrente dada por ψ = a x 2 - b y 2 + c x + d x y , onde a , b , c , e d são constantes. (a) Obtenha expres
Para o campo de velocidade do Problema 9-49, faça o gráfico das linhas de corrente ψ = 0 ,1 ,2 ,3 ,4 ,5 e 6m 2 / s . Considere as constantes a , b e c com os seguintes valores: a = 0,5s - 1 , b = - 1,